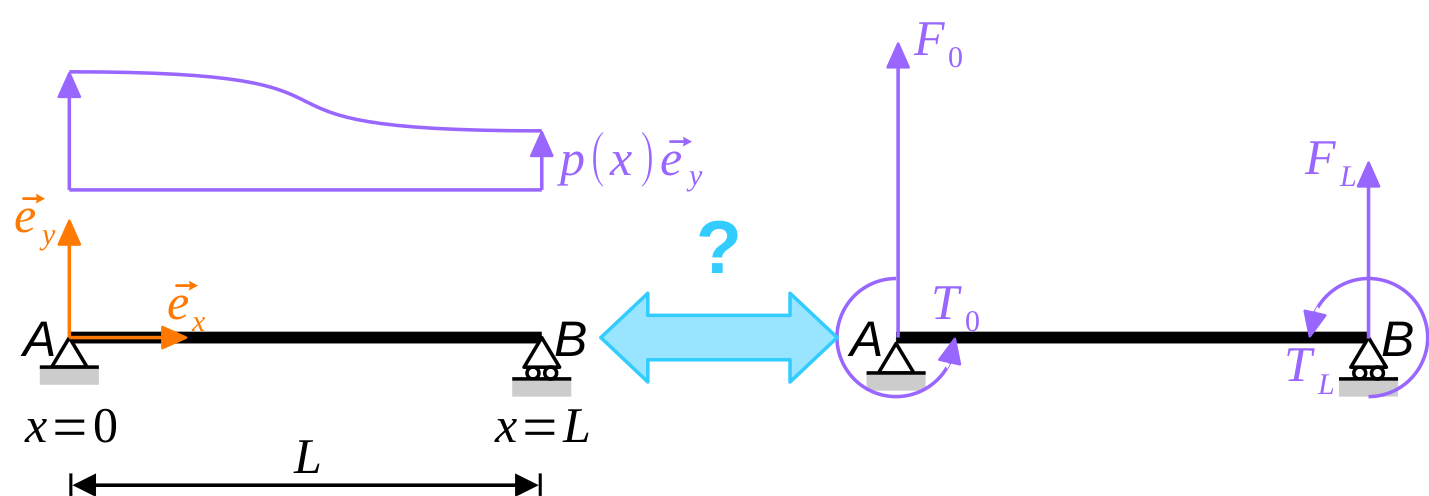
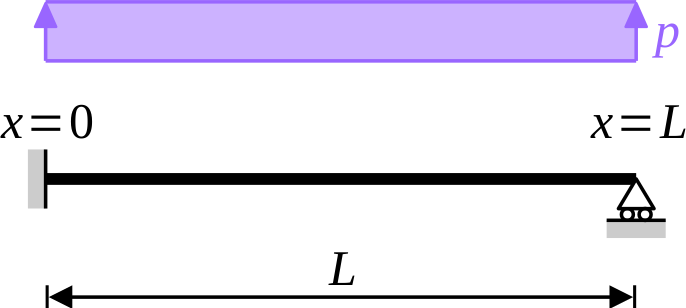
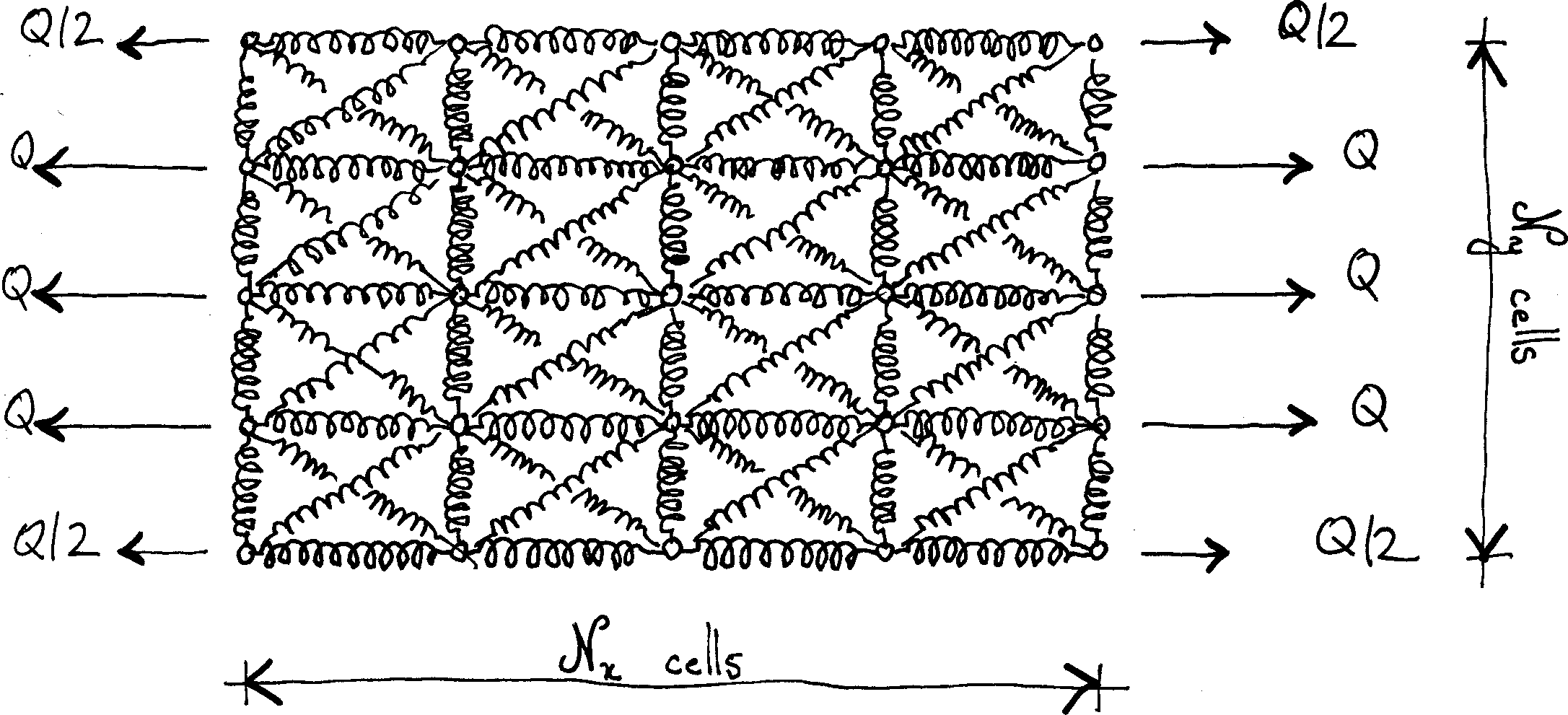
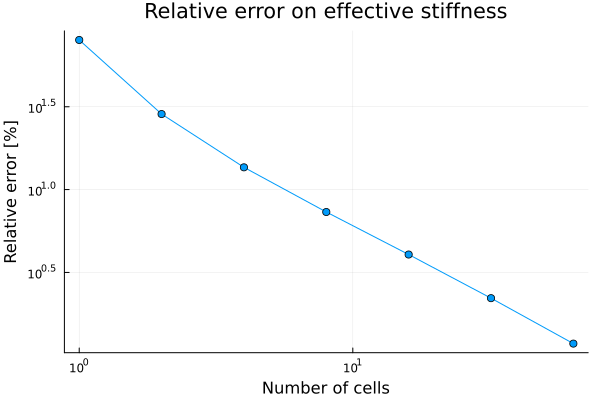
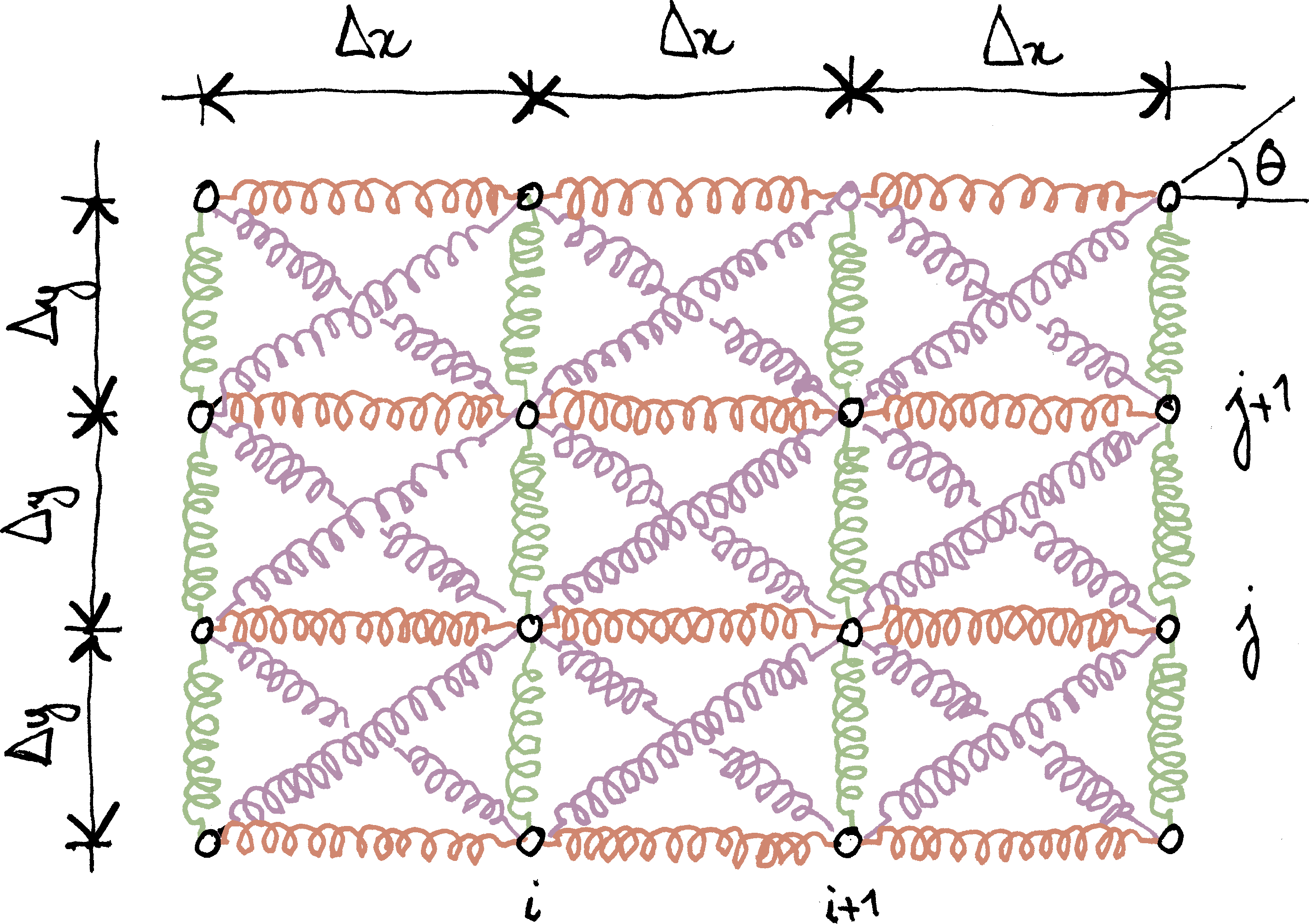
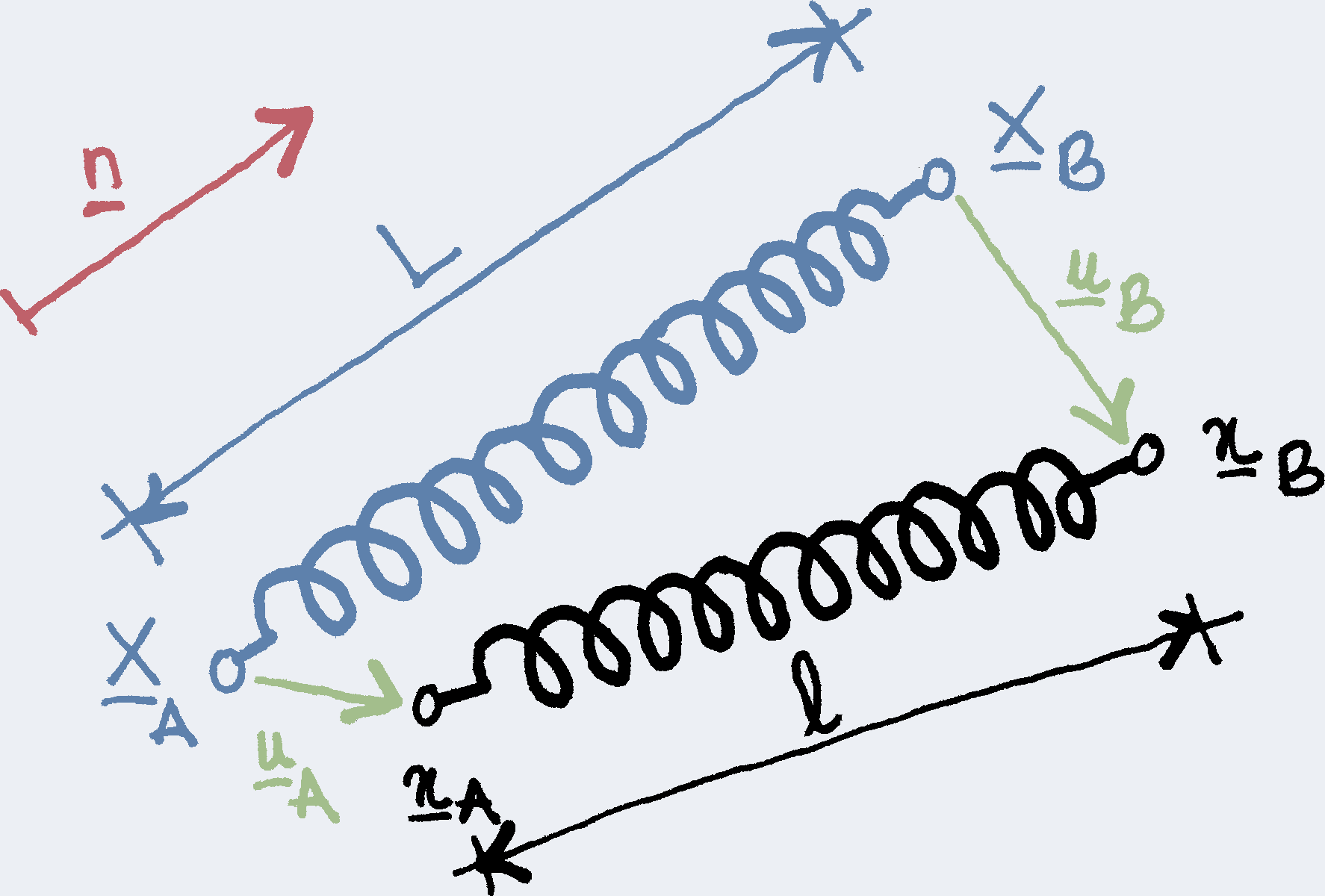
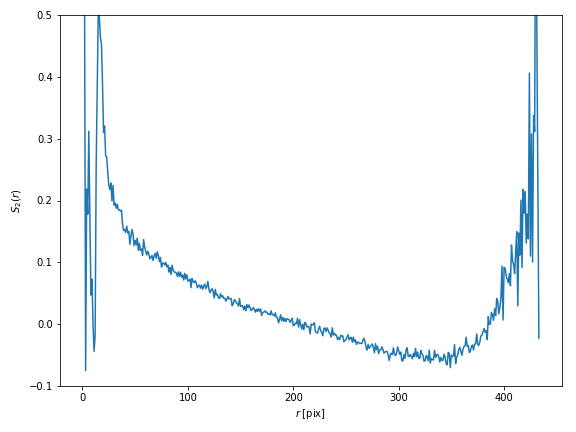
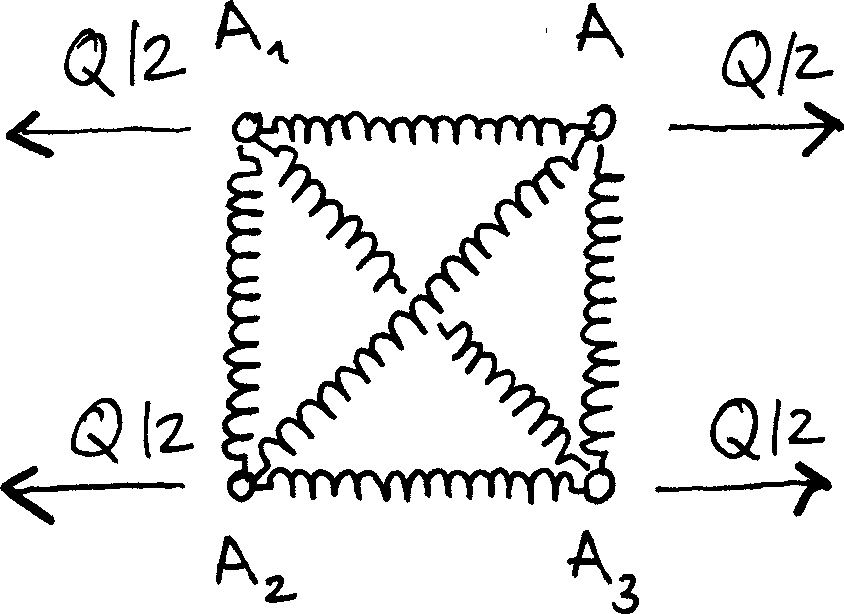Welcome!

You’ve reached the blog of Sébastien Brisard. My most recent posts are listed below.

Please also visit the documentation of some of my projects

https://sbrisard.github.io/janus: the documentation of the Janus library,
https://sbrisard.github.io/pw85: the documentation of the PW85 library.

as well as some recent (work in progress) open books

Enjoy reading!

Numerical analysis of a spring mesh

In this post, we compute numeric values of the apparent stiffness introduced in this post. Our goal is to find the solution to the general problem depicted below.

Sébastien Brisard

Symbolic analysis of a spring mesh

In this post, we compute symbolic expressions of the apparent stiffness introduced in this post. Our goal is to find the solution to the general problem depicted below.

Sébastien Brisard

What is homogenization? Part 5: introducing the representative volume element

In the previous instalment of this series on homogenization, we derived the homogenized properties of a rectangular spring mesh. Our goal in this post is to analyse the…

Sébastien Brisard

What is homogenization? Part 4: a first example

In the previous instalment of this series on homogenization, we discussed volume and ensemble averages for random heterogeneous materials. In view of introducing statistical …

Sébastien Brisard

On the stiffness matrix of a linear spring

This post is not going to be the most exciting I have ever written. We will derive the expression of the elastic energy of a linear spring as a function of the displacement…

Sébastien Brisard

What is homogenization? Part 3: ensemble averages vs. volume averages

In the previous instalment of this series on homogenization, we discussed homogenization of a distribution of black dots on a white background to a uniform shade of gray. In…

Sébastien Brisard

What is homogenization? Part 2: experimental vs. theoretical homogenization

In the previous instalment of this series, we introduced homogenization and the separation of scales. In the present post, we will discuss two strategies to carry out…

Sébastien Brisard

What is homogenization? Part 1: on the separation of scales

Most of my research activities deal with upscaling the mechanical properties of heterogeneous materials. This is also known as homogenization. So what is homogenization?…

Sébastien Brisard

On the periodic-plus-smooth decomposition of an image, part 7: improved implementation of Moisan’s algorithm

In the previous instalment of this series, we implemented Moisan’s (2011) efficient algorithm to compute the periodic-plus-smooth decomposition of an image. This algorithm…

On the periodic-plus-smooth decomposition of an image, part 6: minimizing the energy, the clever way

In the previous instalment of this series, we computed Moisan’s (2011) periodic-plus-smooth decomposition of an image by means of the conjugate gradient method. This worked…

On the periodic-plus-smooth decomposition of an image, part 5: minimizing the energy, the clumsy way

In this post, we will compute Moisan’s (2011) periodic-plus-smooth decomposition of an image by direct minimization of the energy introduced in the second instalment of this…

On the periodic-plus-smooth decomposition of an image, part 4: implementing the linear operators

In the previous instalment of this series, we introduced the linear operators \(Q_1\) and \(Q\) that allow to define Moisan’s (2011) periodic-plus-smooth decomposition \((p…

On the periodic-plus-smooth decomposition of an image, part 3: the energy as a quadratic form

In the previous instalment of this series, we introduced the periodic-plus-smooth decomposition of an image as a pair of images which minimizes an energy functional.…

On the periodic-plus-smooth decomposition of an image, part 2: defining the decomposition

In the previous instalment of this series, we discussed the need for periodic images. Although not all images are periodic, some image analysis techniques are best performed…

On the periodic-plus-smooth decomposition of an image, part 1: introduction

In this new series, we will explore the so-called periodic-plus-smooth decomposition of an image, introduced by Moisan in 2011. This series is largely based on Moisan’s…

Orientation correlations among rice grains, part 8: estimating the correlations

In the previous instalment of this series, we have analyzed the morphology of the rice grains. In particular, we have defined their orientation as that of the major axis of…

Orientation correlations among rice grains, part 7: analysis of the shape of the grains

In the previous instalment of this series, we have segmented the 3D image of the assembly of rice grains. In other words, each voxel of the image is attributed the label of…

Orientation correlations among rice grains, part 6: segmentation

In the previous instalment of this series, I showed that a convincing binary image could be produced from the gray level 3D reconstruction of the assembly of rice grains…

Orientation correlations among rice grains, part 5: thresholding

In the previous instalment of this series, we used the circle Hough transform to find the boundary of the sample and define the circular ROI. Within this ROI, we now need to…

When a thin shell is not so thin, part 3: the thick shell solution

Finding the stress resultant and stress couple in a spherical pressure vessel seems easy enough. Well, this apparently simple problem allows us to highlight subtle thickness…

When a thin shell is not so thin, part 2: the 3D, exact solution

In the previous instalment of this series, we analysed a spherical pressure vessel by means of Koiter’s linear theory of thin shells. We found the somewhat unexpected result…

When a thin shell is not so thin, part 1: Koiter’s linear theory

In structural analysis, thick beams (resp. plates) usually refer to shear deformability, and the Timoshenko beam theory (resp. Mindlin–Reissner plate theory). With curved…

Orientation correlations among rice grains, part 4: defining the ROI

In the previous instalment of this series, we obtained binned slices of the sample. Fig. 1 below displays a typical example of these binned slices. We now want to segment…

Orientation correlations among rice grains, part 3: intermezzo – Binning images

The full reconstructed image resulting from the tomography experiment described in the second instalment of this series is a 1747×1751×688 stack. The voxel size is about…

Orientation correlations among rice grains, part 2: acquisition of tomography images

In the first instalment of this series, I briefly introduced orientational order in assemblies of anisotropic particles, and proposed an illustration based on synthetic…

Orientation correlations among rice grains, part 1: introduction

In this series, I will explore the notion of orientational order in random packings of anisotropic (flat or elongated), hard particles. By orientational order, I mean that…

Decomposition of transverse isotropic, fourth-rank tensors

In a previous post, I introduced the fourth-rank spherical and deviatoric projection tensors. Any isotropic fourth-rank tensor is a linear combination of these two tensors;…

On the double dot product

The double dot product of two tensors is the contraction of these tensors with respect to the last two indices of the first one, and the first two indices of the second one.…

The elastic acoustic tensor and its inverse

In this post, I will introduce the acoustic tensor of linearly elastic materials. Closed-form expressions of the inverse of this tensor can be derived in the case of isotropic…

Elastic constants of an isotropic material, part 3: putting it all together

In the previous instalments of this series (see Part 1 and Part 2), I have shown that regardless of the dimensionality (3D or plane strain elasticity), the constitutive law…

Elastic constants of an isotropic material, part 2: plane strain elasticity

In the previous instalment of this series, I introduced the constitutive law of an isotropically elastic material, and the related material constants, within the framework…

Elastic constants of an isotropic material, part 1: 3D elasticity

Among all classes of materials, the class of linearly elastic and isotropic materials is the simplest. Such materials are defined by two elastic constants: for example…