Implementation of the function f¶
In this chapter, we explain how the contact function is computed. From
Eq. (12) in chapter Theory, the value of
the contact function is found from the solution λ to equation
f'(λ) = 0, where it is recalled that f is defined as follows:
(1) f(λ) = λ(1-λ)r₁₂ᵀ⋅Q⁻¹⋅r₁₂,
with:
(2) Q = (1-λ)Q₁ + λQ₂.
In the present chapter, we discuss two implementations for the
evaluation of f. The first implementation uses the Cholesky decomposition of
Q. The second implementation uses a representation of f as
a quotient of two polynomials (rational fraction).
Implementation #1: using Cholesky decompositions¶
Since Q is a symmetric, positive definite matrix, we can compute
its Cholesky decomposition, which reads
as follows:
(3) Q = L⋅Lᵀ,
where L is a lower-triangular matrix. Using this decomposition, it
is straightforward to compute s = Q⁻¹⋅r (where we write r as a
shorthand for r₁₂), so that:
(4) f(λ) = λ(1-λ)rᵀ⋅s.
In order to solve f′(λ) = 0 numerically, we use a Newton–Raphson procedure, which
requires the first and second derivatives of f. It is readily
found that:
(5) s′ = -Q⁻¹⋅Q′⋅Q⁻¹⋅r = -Q⁻¹⋅u and rᵀ⋅s′ = -rᵀ⋅Q⁻¹⋅u = -sᵀ⋅u,
with u = Q₁₂⋅s and Q₁₂ = Q₂-Q₁. Therefore:
(6) f′(λ) = (1-2λ)rᵀ⋅s - λ(1-λ)sᵀ⋅u.
Similarly, introducing v = Q⁻¹⋅u:
(7) sᵀ⋅u′ = sᵀ⋅Q₁₂⋅s′ = -sᵀ⋅Q₁₂⋅Q⁻¹⋅u = -uᵀ⋅v,
and:
(8) uᵀ⋅s′ = -uᵀ⋅Q⁻¹⋅u = -uᵀ⋅v.
Therefore:
(9) f″(λ) = -2rᵀ⋅s - 2(1-2λ)sᵀ⋅u + 2λ(1-λ)uᵀ⋅v.
Implementation #2: using rational functions¶
We observe that f(λ) is a
rational function [see Eq. (1)], and we write:
λ(1-λ)a(λ)
(10) f(λ) = ──────────,
b(λ)
with:
(11a) a(λ) = r₁₂ᵀ⋅adj[(1-λ)Q₁+λQ₂]⋅r₁₂ = a₀ + a₁λ + a₂λ²,
(11b) b(λ) = det[(1-λ)Q₁+λQ₂] = b₀ + b₁λ + b₂λ² + b₃λ³,
where adj(Q) denotes the adjugate matrix of Q (transpose of its cofactor
matrix), see e.g Wikipedia.
The coefficients aᵢ and bᵢ are found from the evaluation of a(λ) and
b(λ) for specific values of λ:
(12a) a₀ = a(0),
a(1) - a(-1)
(12b) a₁ = ────────────,
2
a(1) + a(-1)
(12c) a₂ = ──────────── - a(0),
2
(12d) b₀ = b(0),
8b(½) b(1) b(-1)
(12e) b₁ = ───── - 2b(0) - ──── - ─────
3 2 6
b(1) + b(-1)
(12f) b₂ = ──────────── - b(0),
2
8b(½) b(-1)
(12g) b₃ = -───── + 2b(0) + b(1) - ─────.
3 3
This requires the implementation of the determinant and the adjugate matrix of a
3×3, symmetric matrix, see pw85__det_sym() and
pw85__xT_adjA_x().
Evaluating the derivative of f with respect to λ is fairly easy. The following Sympy script will do the job:
import sympy
from sympy import Equality, numer, pprint, Symbol
if __name__ == '__main__':
sympy.init_printing(use_latex=False, use_unicode=True)
λ = Symbol('λ')
a = sum(sympy.Symbol('a{}'.format(i))*λ**i for i in range(3))
b = sum(sympy.Symbol('b{}'.format(i))*λ**i for i in range(4))
f = λ*(1-λ)*a/b
f_prime = f.diff(λ).ratsimp()
c = numer(f_prime)
c_dict = c.collect(λ, evaluate=False)
for i in range(sympy.degree(c, gen=λ)+1):
pprint(Equality(Symbol('c{}'.format(i)), c_dict[λ**i]))
It is readily found that:
c(λ)
(13) f′(λ) = ───────,
b(λ)²
where c(λ) is a sixth-order polynomial in λ:
(14) c(λ) = c₀ + c₁λ + c₂λ² + c₃λ³ + c₄λ⁴ + c₅λ⁵ + c₆λ⁶,
with:
(15a) c₀ = a₀b₀,
(15b) c₁ = 2(a₁-a₀)b₀,
(15c) c₂ = -a₀(b₁+b₂) + 3b₀(a₂-a₁) + a₁b₁,
(15d) c₃ = 2[b₁(a₂-a₁) - a₀b₃] - 4a₂b₀,
(15e) c₄ = (a₀-a₁)b₃ + (a₂-a₁)b₂ - 3a₂b₁,
(15f) c₅ = -2a₂b₂,
(15g) c₆ = -a₂b₃,
Solving f'(λ) = 0 for λ is therefore equivalent to finding the unique
root of c in the interval 0 ≤ λ ≤ 1. For the sake of robustness, the
bisection method has been
implemented (more efficient methods will be implemented in future versions).
Once λ is found, μ is computed from μ² = f(λ) using Eq. (10).
Comparison of the two implementations¶
High precision reference data was generated using the mpmath library. The reference dataset is fully described and
freely downloadable from the Zenodo platform
(DOI:10.5281/zenodo.3323683). Accuracy of both implementations is
then evaluated through the following script (download source file):
#include <glib.h>
#include <hdf5.h>
#include <hdf5_hl.h>
#include <pw85.h>
#include <pw85_legacy.h>
void read_dataset_double(hid_t const hid, char const *dset_name, size_t *size,
double **buffer) {
int ndims;
H5LTget_dataset_ndims(hid, dset_name, &ndims);
hsize_t *dim = g_new(hsize_t, ndims);
H5LTget_dataset_info(hid, dset_name, dim, NULL, NULL);
*size = 1;
for (size_t i = 0; i < ndims; i++) {
*size *= dim[i];
}
*buffer = g_new(double, *size);
H5LTread_dataset_double(hid, dset_name, *buffer);
g_free(dim);
}
void update_histogram(double act, double exp, size_t num_bins, size_t *hist) {
double const err = fabs((act - exp) / exp);
int prec;
if (err == 0.0) {
prec = num_bins - 1;
} else {
prec = (int)(floor(-log10(err)));
if (prec <= 0) {
prec = 0;
}
if (prec >= num_bins) {
prec = num_bins - 1;
}
}
++hist[prec];
}
int main() {
hid_t const hid = H5Fopen(PW85_REF_DATA_PATH, H5F_ACC_RDONLY, H5P_DEFAULT);
size_t num_directions;
double *directions;
read_dataset_double(hid, "/directions", &num_directions, &directions);
num_directions /= PW85_DIM;
size_t num_lambdas;
double *lambdas;
read_dataset_double(hid, "/lambdas", &num_lambdas, &lambdas);
size_t num_radii;
double *radii;
read_dataset_double(hid, "/radii", &num_radii, &radii);
size_t num_spheroids;
double *spheroids;
read_dataset_double(hid, "/spheroids", &num_spheroids, &spheroids);
num_spheroids /= PW85_SYM;
size_t num_expecteds;
double *expecteds;
read_dataset_double(hid, "/F", &num_expecteds, &expecteds);
double *exp = expecteds;
double params[2 * PW85_SYM + PW85_DIM];
size_t num_bins = 16;
size_t hist1[num_bins];
size_t hist2[num_bins];
for (size_t i = 0; i < num_bins; i++) {
hist1[i] = 0;
hist2[i] = 0;
}
for (size_t i1 = 0; i1 < num_spheroids; i1++) {
memcpy(params + PW85_DIM, spheroids + PW85_SYM * i1,
PW85_SYM * sizeof(double));
for (size_t i2 = 0; i2 < num_spheroids; i2++) {
memcpy(params + PW85_DIM + PW85_SYM, spheroids + PW85_SYM * i2,
PW85_SYM * sizeof(double));
for (size_t i = 0; i < num_directions; i++) {
memcpy(params, directions + PW85_DIM * i, PW85_DIM * sizeof(double));
for (size_t j = 0; j < num_lambdas; j++, exp++) {
double const act1 = -pw85_f_neg(lambdas[j], params);
update_histogram(act1, *exp, num_bins, hist1);
double out[2];
pw85_legacy_f2(lambdas[j], params, params + PW85_DIM,
params + PW85_DIM + PW85_SYM, out);
double const act2 = out[0];
update_histogram(act2, *exp, num_bins, hist2);
}
}
}
}
FILE *f = fopen(HISTOGRAM_PATH, "w");
for (size_t i = 0; i < num_bins; i++) {
fprintf(f, "%d,%g,%g\n", (int)i,
100. * ((double)hist1[i]) / ((double)num_expecteds),
100. * ((double)hist2[i]) / ((double)num_expecteds));
}
fclose(f);
g_free(spheroids);
g_free(radii);
g_free(lambdas);
g_free(directions);
H5Fclose(hid);
return 0;
}
Note
To compute this program, you might need to pass the options
-Dpw85_include=…, -Dpw85_lib=… and -Dpw85_data=…
to meson.
Note
The provided script refers to an old implementation of pw85.
We get the histograms shown in Fig. 1. These histograms show that Implementation #1 is more accurate than Implementation #2. The former will therefore be selected as default.
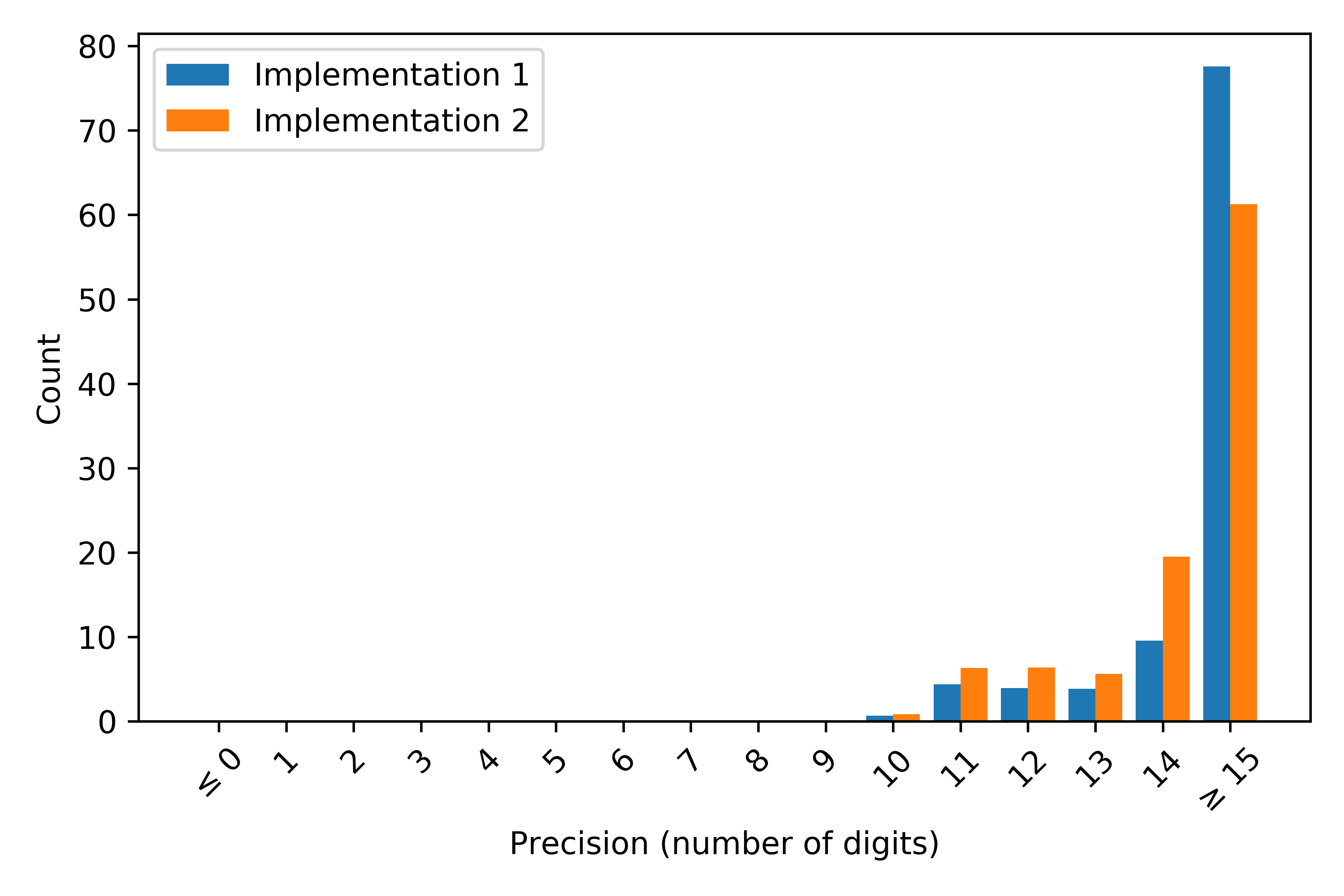
Fig. 1 Accuracy of the two implementations.¶