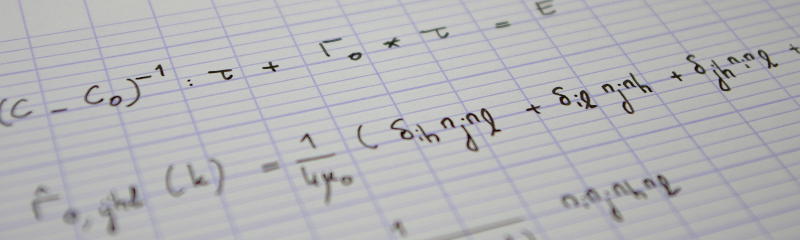One of my manuscripts has just been accepted for publication in the International Journal of Solids and Structures. It is called A variational form of the equivalent inclusion method for numerical homogenization. The abstract is reproduced below
Due to its relatively low computational cost, the equivalent inclusion method is an attractive alternative to traditional full-field computations of heterogeneous materials formed of simple inhomogeneities (spherical, ellipsoidal) embedded in a homogeneous matrix. The method can be seen as the discretization of the Lippmann--Schwinger equation with piecewise polynomials. Contrary to the original approach of Moschovidis and Mura, who discretized the strong form of the Lippmann--Schwinger equation through Taylor expansions, we propose in the present paper a Galerkin discretization of the weak form of this equation. Combined with the new, mixed boundary conditions recently introduced by the authors, the resulting method is particularly well-suited to homogenization. It is shown that this new, variational approach has a number of benefits: (i) the resulting linear system is well-posed, (ii) the numerical solution converges to the exact solution as the maximum degree of the polynomials tends to infinity and (iii) the method can provide rigorous bounds on the apparent properties of the statistical volume element, provided that the matrix is stiffer (or softer) than all inhomogeneities. This paper presents the formulation and implementation of the new, variational form of the equivalent inclusion method. Its efficiency is investigated through numerical applications in 2D and 3D elasticity.
See the preprint on HAL and the published version.