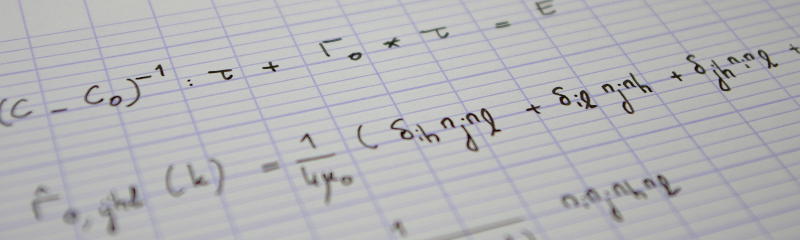In this post, I will introduce the acoustic tensor of linearly elastic materials. Closed-form expressions of the inverse of this tensor can be derived in the case of isotropic materials. This will later come in handy to derive closed-form expressions of the periodic Green operator for strains.
We consider a linearly elastic material with stiffness $\tens C$. For any wave-vector $\vec k$, the elastic acoustic tensor $\tens A(\vec k)$ is defined as follows
$$\tens A(\vec k)=\vec k\cdot\tens C\cdot\vec k=k^2\vec n\cdot\tens C\cdot\vec n,\tag{1}$$
where $k$ is the amplitude of the wave-vector $\vec k$, $k=\sqrt{\vec k\cdot\vec k}$, and $\vec n$ is its direction ($\vec k=k\vec n$). The acoustic tensor is used to assess material stability (Bigoni and Zaccaria, European Journal of Mechanics- A/Solids 13(5), pp. 621–638, 1994) and study the propagation of waves (Gentile and Straughan, 2013). As far as we are concerned, the derivation of the periodic Green operator for strains will require the expressions of the inverse of the acoustic tensor. This is the topic of the present post, which is restricted to isotropic materials: the stiffness tensor $\tens C$ of isotropic materials is therefore a linear combination of the isotropic projection tensors $\tens J$, and $\tens K$
$$\tens C=d\kappa\tens J+2\mu\tens K.\tag{2}$$
To compute the elastic acoustic tensor, we therefore need to find the expressions of $\vec n\cdot\tens J\cdot\vec n$ and $\vec n\cdot\tens K\cdot\vec n$, for any unit vector $\vec n$. We start with the computation of $\vec n\cdot\tens I\cdot\vec n$, where $\tens I$ denotes the fourth-rank identity tensor. We have
$$\bigl(\vec n\cdot\tens I\cdot\vec n\bigr)_{jk}=n_iI_{ijkl}n_l=n_in_l\frac12\bigl(\delta_{il}\delta_{jk}+\delta_{jl}\delta_{ik}\bigr)=\frac12\bigl(n_in_i\delta_{jk}+n_jn_k\bigr).$$
Since $\vec n$ is a unit vector, we have $n_in_i=1$, and
$$\vec n\cdot\tens I\cdot\vec n=\frac12\bigl(\tens\delta+\vec n\otimes\vec n\bigr),$$
where $\tens\delta$ denotes the second-rank identity tensor. It will be convenient to introduce the projectors $\tens p$ and $\tens q$, defined as follows
$$\tens p=\vec n\otimes\vec n\quad\text{and}\quad\tens q=\tens\delta-\tens p,$$
or, using indices
$$p_{ij}=n_in_j\quad\text{and}\quad q_{ij}=\delta_{ij}-n_in_j.$$
It can readily be verified that
$$\tens p\cdot\tens p=\tens p,\quad\tens q\cdot\tens q=\tens q\quad\text{and}\quad\tens p\cdot\tens q=\tens q\cdot\tens p=\tens0,\tag{3}$$
and
$$\vec n\cdot\tens I\cdot\vec n=\tens p+\frac12\tens q.\tag{4}$$
Similarly
$$\vec n\cdot\tens J\cdot\vec n=\frac1d\vec n\cdot\bigl(\tens\delta\otimes\tens\delta\bigr)\cdot\vec n=\frac1d\vec n\otimes\vec n=\frac1d\tens p.\tag{5}$$
Finally, combining identity $\tens K=\tens I-\tens J$ with Eqs. (4) and (5)
$$\vec n\cdot\tens K\cdot\vec n=\frac{d-1}d\tens p+\frac12\tens q.\tag{6}$$
The acoustic tensor of an elastic, linear, isotropic material is obtained from Eqs. (1), (2), (5) and (6)
$$\tens A(\vec n)=\Bigl(\kappa+2\mu\frac{d-1}d\Bigr)\tens p+\mu\tens q.$$
From this post, it can readily be verified that
$$\kappa+2\mu\frac{d-1}d=2\mu\frac{1-\nu}{1-2\nu},$$
this identity being true in both 3D and plane strain elasticity. The acoustic tensor therefore reads
$$\tens A(\vec k)=k^2\mu\Bigl[\frac{2\bigl(1-\nu\bigr)}{1-2\nu}\tens p+\tens q\Bigr].$$
Finally, using the properties of the projectors $\tens p$ and $\tens q$ [see Eq. (3)], the inverse of the acoustic tensor can be derived
$$\tens A^{-1}(\vec k)=\frac1{k^2\mu}\Bigl[\frac{1-2\nu}{2\bigl(1-\nu\bigr)}\tens p+\tens q\Bigr].$$