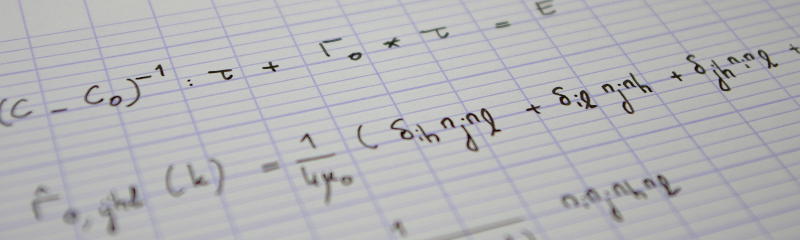In a previous post, I introduced the fourth-rank spherical and deviatoric projection tensors. Any isotropic fourth-rank tensor is a linear combination of these two tensors; in other words, the space of isotropic fourth-rank tensors (with minor and major symmetries) is of dimension 2. Similarly, it can be shown (Walpole, 1984) that the space of three-dimensional, transverse isotropic fourth-rank tensors (with minor and major symmetries) is of dimension 6. Furthermore; it is possible to produce a convenient basis of this space. This is the topic of the present post, which is mostly based on the paper by Walpole (1984).
Two second-rank projection tensors
It is recalled that transverse isotropy is defined by one single preferred direction. In the present post, $\vec n$ denotes the unit vector which indicates this preferred direction. Then, $\tens p$ and $\tens q$ are the following projectors
$$\tens p=\vec n\otimes\vec n,\quad\tens q=\tens{\delta}-\tens p.\tag{1}$$
$\tens p$ is the projector onto the direction of anisotropy $\vec n$, while $\tens q$ is the projection onto the plane of isotropy (orthogonal to $\vec n$). It can readily be verified that
$$\tens p\cdot\tens p=\tens p,\quad\tens q\cdot\tens q=\tens q,\quad\tens p\cdot\tens q=\tens q\cdot\tens p=\tens 0$$
and
$$\tens p\dbldot\tens p=1,\quad\tens q\dbldot\tens q=2,\quad\tens p\dbldot\tens q=\tens q\dbldot\tens p=0.$$
Tensor product of linear transformations
It will be convenient to introduce a new, Kronecker-like product of two second-rank tensors, which Del Piero (1979) named tensor product of linear transformations, and which will be denoted $\boxtimes{}$.
As a preliminary note, it should be observed that any fourth-rank tensor $\tens A$ can be viewed as a endomorphism over the space of second-rank tensors, since $\tens x\mapsto\tens A\dbldot\tens x$ is a linear mapping (the convention adopted in this blog for the double dot product has been specified in a previous post). Therefore, the fourth-rank tensor $\tens a\boxtimes\tens b$ ($\tens a, \tens b$: second-rank tensors) can be defined by how it operates on second-rank tensors $\tens x$
$$\bigl(\tens a\boxtimes\tens b\bigr)\dbldot\tens x=\tens a\cdot\tens x\cdot\transp{\tens b}.\tag{2}$$
Writing the above definition in terms of the components of $\tens a$, $\tens b$ and $\tens x$, it is found that $\bigl(\tens a\boxtimes\tens b\bigr)\dbldot\tens x=a_{ik}x_{kl}b_{jl}\vec e_i\otimes\vec e_j$, which shows that the components of $\tens a\boxtimes\tens b$ are
$$\bigl(\tens a\boxtimes\tens b\bigr)_{ijkl}=a_{ik}b_{jl},\tag{3}$$
from which it results
$$\bigl(\tens a\boxtimes\tens b\bigr)^{\mathsf{T}}=\tens a^{\mathsf{T}}\boxtimes\tens b^{\mathsf{T}}.$$
Given four second-rank tensors $\tens a$, $\tens b$, $\tens c$ and $\tens d$, the following identity holds
$$\bigl(\tens a\boxtimes\tens b\bigr)\dbldot\bigl(\tens c\boxtimes\tens d\bigr)=\bigl(\tens a\cdot\tens c\bigr)\boxtimes\bigl(\tens b\cdot\tens d\bigr).\tag{4}$$
Indeed, let $\tens x$ be a second-rank tensor. Then, from Eq. (2)
$$\bigl(\tens a\boxtimes\tens b\bigr)\dbldot\bigl(\tens c\boxtimes\tens d\bigr)\dbldot\tens x=\bigl(\tens a\boxtimes\tens b\bigr)\dbldot\bigl(\tens c\cdot\tens x\cdot\tens d^{\mathsf{T}}\bigr)=\tens a\cdot\bigl(\tens c\cdot\tens x\cdot\tens d^{\mathsf{T}}\bigr)\cdot\tens b^{\mathsf{T}}$$ $$=\bigl(\tens a\cdot\tens c\bigr)\cdot\tens x\cdot\bigl(\tens d^{\mathsf{T}}\cdot\tens b^{\mathsf{T}}\bigr)=\bigl(\tens a\cdot\tens c\bigr)\cdot\tens x\cdot\bigl(\tens b\cdot\tens d\bigr)^{\mathsf{T}}$$ $$=\bigl[\bigl(\tens a\cdot\tens c\bigr)\boxtimes\bigl(\tens b\cdot\tens d\bigr)\bigr]\dbldot\tens x.$$
Eq. (3) shows that even if $\tens a$ and $\tens b$ are symmetric, the tensor product $\tens a\boxtimes\tens b$ does not necessarily have the minor symmetries. It will therefore be convenient to define $\tens a\overset{\mathrm s}{\boxtimes}\tens b$, as the tensor $\tens a\boxtimes\tens b$, symmetrized with respect to the last two indices
$$\bigl(\tens a\overset{\mathrm s}{\boxtimes}\tens b\bigr)_{ijkl}=\frac12\bigl(a_{ik}b_{jl}+a_{il}b_{jk}\bigr),$$
or, in intrinsic form ($\tens x$: second-rank tensor)
$$\bigl(\tens a\overset{\mathrm s}{\boxtimes}\tens b\bigr)\dbldot\tens x=\frac12\bigl(\tens a\boxtimes\tens b\bigr)\dbldot\bigl(\tens x+\tens x^{\mathsf T}\bigr)=\frac12\tens a\cdot\bigl(\tens x+\tens x^{\mathsf T}\bigr)\cdot\tens b^{\mathsf T}.\tag{5}$$
An identity similar to Eq. (4) can then be derived with $\overset{\mathrm s}{\boxtimes}$
$$\bigl(\tens a\overset{\mathrm s}{\boxtimes}\tens b\bigr)\dbldot\bigl(\tens c\overset{\mathrm s}{\boxtimes}\tens d\bigr)=\frac12\bigl[\bigl(\tens a\cdot\tens c\bigr)\overset{\mathrm s}{\boxtimes}\bigl(\tens b\cdot\tens d\bigr)+\bigl(\tens a\cdot\tens d\bigr)\overset{\mathrm s}{\boxtimes}\bigl(\tens b\cdot\tens c\bigr)\bigr].\tag{6}$$
The following identities, involving the second-rank projectors $\tens p$ and $\tens q$ [see Eq. (1)], readily follow from Eq. (3)
$$\bigl(\tens p\overset{\mathrm s}{\boxtimes}\tens p\bigr)\dbldot\tens p=\tens p,\quad\bigl(\tens p\overset{\mathrm s}{\boxtimes}\tens p\bigr)\dbldot\tens q=\tens 0,$$
$$\bigl(\tens q\overset{\mathrm s}{\boxtimes}\tens q\bigr)\dbldot\tens p=\tens 0,\quad\bigl(\tens q\overset{\mathrm s}{\boxtimes}\tens q\bigr)\dbldot\tens q=\tens q,$$
and
$$\bigl(\tens p\overset{\mathrm s}{\boxtimes}\tens q\bigr)\dbldot\tens p=\bigl(\tens p\overset{\mathrm s}{\boxtimes}\tens q\bigr)\dbldot\tens q=\bigl(\tens q\overset{\mathrm s}{\boxtimes}\tens p\bigr)\dbldot\tens p=\bigl(\tens q\overset{\mathrm s}{\boxtimes}\tens p\bigr)\dbldot\tens q=\tens 0.$$
Besides, the following multiplication table results from Eq. (6) $\newcommand{\x}{\overset{\mathrm s}{\boxtimes}}$
| $\dbldot$ | $\tens p\overset{\mathrm s}{\boxtimes}\tens p$ | $\tens p\overset{\mathrm s}{\boxtimes}\tens q$ | $\tens q\overset{\mathrm s}{\boxtimes}\tens p$ | $\tens q\overset{\mathrm s}{\boxtimes}\tens q$ |
|---|---|---|---|---|
| $\tens p\overset{\mathrm s}{\boxtimes}\tens p$ | $\tens p\overset{\mathrm s}{\boxtimes}\tens p$ | $\tens 0$ | $\tens 0$ | $\tens 0$ |
| $\tens p\overset{\mathrm s}{\boxtimes}\tens q$ | $\tens 0$ | $\tens 0$ | $\tens 0$ | $\tens 0$ |
| $\tens q\overset{\mathrm s}{\boxtimes}\tens p$ | $\tens 0$ | $\tens 0$ | $\tens 0$ | $\tens 0$ |
| $\tens q\overset{\mathrm s}{\boxtimes}\tens q$ | $\tens 0$ | $\tens 0$ | $\tens 0$ | $\tens q\overset{\mathrm s}{\boxtimes}\tens q$ |
To conclude, it is observed that the fourth-rank tensor $\tens{I}=\tens{\delta}\overset{\mathrm s}{\boxtimes}\tens{\delta}$ maps any second-rank tensor to its symmetric part: it reduces to the identity tensor over the space of second-rank, symmetric tensors.
Walpole\'s basis for transverse isotropic tensors
Walpole (1984) shows that any transverse isotropic tensor is a linear combination of the six fourth-rank tensors $\tens E_1$, $\tens E_2$, $\tens E_3$, $\tens E_4$, $\tens F$ and $\tens G$ defined as follows
$$\tens E_1=\tens p\otimes\tens p,\quad\tens E_2=\frac12\tens q\otimes\tens q,\quad\tens E_3=\frac1{\sqrt2}\tens p\otimes\tens q,\quad\tens E_4=\frac1{\sqrt2}\tens q\otimes\tens p$$ $$\tens F=\tens q\overset{\mathrm s}{\boxtimes}\tens q-\frac12\tens q\otimes\tens q,\quad\tens G=\tens p\overset{\mathrm s}{\boxtimes}\tens q+\tens q\overset{\mathrm s}{\boxtimes}\tens p.$$
Multiplication (in the sense of the double product) of these tensors is fairly easy, as shown by the table below.
| $\dbldot$ | $\tens E_1$ | $\tens E_2$ | $\tens E_3$ | $\tens E_4$ | $\tens F$ | $\tens G$ |
|---|---|---|---|---|---|---|
| $\tens E_1$ | $\tens E_1$ | $\tens 0$ | $\tens E_3$ | $\tens 0$ | $\tens 0$ | $\tens 0$ |
| $\tens E_2$ | $\tens 0$ | $\tens E_2$ | $\tens 0$ | $\tens E_4$ | $\tens 0$ | $\tens 0$ |
| $\tens E_3$ | $\tens 0$ | $\tens E_3$ | $\tens 0$ | $\tens E_1$ | $\tens 0$ | $\tens 0$ |
| $\tens E_4$ | $\tens E_4$ | $\tens 0$ | $\tens E_2$ | $\tens 0$ | $\tens 0$ | $\tens 0$ |
| $\tens F$ | $\tens 0$ | $\tens 0$ | $\tens 0$ | $\tens 0$ | $\tens F$ | $\tens 0$ |
| $\tens G$ | $\tens 0$ | $\tens 0$ | $\tens 0$ | $\tens 0$ | $\tens 0$ | $\tens G$ |
The above table must be read as: “row double dot column equals cell”. For example, $\tens E_1:\tens E_3=\tens E_3$ and $\tens E_3:\tens E_1=\tens 0$.
A convenient representation of transverse isotropic, fourth-rank tensors
Walpole (1984) proposes a convenient representation of any transverse isotropic tensor $\tens T$, as the triplet $(A, f, g)$ where $A$ is a 2×2 matrix and $f$ and $g$ are two scalars. This representation should be understood as
$$\tens T=a_{11}\tens E_1+a_{22}\tens E_2+a_{12}\tens E_3+a_{21}\tens E_4+f\tens F+g\tens G,$$
where $a_{ij}$ are the coefficients of $A$. The condensed notation $\tens T=(A, f, g)$ shall be adopted. Using the above multiplication table, it can readily be verified that if $\tens T=(A, f, g)$ and $\tens T'=(A', f', g')$, then
$$\tens T\dbldot\tens T'=(A\cdot A', ff', gg').$$
This representation is particularly convenient when it comes to inverting transverse isotropic tensors. Indeed,
$$\tens T^{-1}=(A^{-1}, 1/f, 1/g).$$
Transposition is also straightforward
$$\tens T^{\mathsf T}=(A^{\mathsf T}, f, g).$$
Decomposition of fourth-rank, isotropic tensors in Walpole\'s basis
The isotropic tensors $\tens{I}$, $\tens{J}$ and $\tens{K}$ introduced previously can be considered as transverse isotropic tensors. As such, they can be decomposed in Walpole\'s basis. First, the identity tensor $\tens{I}$ decomposes as follows
$$\tens{I}=\tens{\delta}\overset{\mathrm s}{\boxtimes}\tens{\delta}=\bigl(\tens p+\tens q\bigr)\overset{\mathrm s}{\boxtimes}\bigl(\tens p+\tens q\bigr)$$ $$=\tens p\overset{\mathrm s}{\boxtimes}\tens p+\tens p\overset{\mathrm s}{\boxtimes}\tens q+\tens q\overset{\mathrm s}{\boxtimes}\tens p+\tens q\overset{\mathrm s}{\boxtimes}\tens q$$ $$=\tens E_1+\tens G+\tens F+\tens E_2.$$
where the identity $\tens p\overset{\mathrm s}{\boxtimes}\tens p=\tens p\otimes\tens p=\tens E_1$ has been used. Now, the decomposition of $\tens{J}$ is readily derived from its definition
$$3\tens{J}=\tens{\delta}\otimes\tens{\delta}=\bigl(\tens p+\tens q\bigr)\otimes\bigl(\tens p+\tens q\bigr)$$ $$=\tens p\otimes\tens p+\tens p\otimes\tens q+\tens q\otimes\tens p+\tens q\otimes\tens q$$ $$=\tens E_1+\sqrt2\tens E_3+\sqrt2\tens E_4+2\tens E_2.$$
Finally, the decomposition of the deviatoric projection tensor $\tens{K}$ is found from the definition $\tens{K}=\tens{I}-\tens{J}$. To sum up
$$\tens{I}=\bigl(\bigl[\begin{smallmatrix}1&0\\ 0&1\end{smallmatrix}\bigr], 1, 1\bigr),$$ $$\tens{J}=\bigl(\tfrac13\bigl[\begin{smallmatrix}1&\sqrt2\\\sqrt2&2\end{smallmatrix}\bigr], 0, 0\bigr),$$ $$\tens{K}=\bigl(\tfrac13\bigl[\begin{smallmatrix}2&-\sqrt2\\-\sqrt2&1\end{smallmatrix}\bigr], 1, 1\bigr).$$
Conclusion
In the present post, a convenient decomposition of three-dimensional, fourth-rank, transverse isotropic tensors as a linear combination of six basis tensors has been proposed. Multiplication (in the sense of the double dot product) of these basis tensors is straightforward. Besides, representing transverse isotropic tensors as a (matrix, scalar, scalar) triplet eases their multiplication and inversion. Walpole's basis turns out to be very handy in many situations (including the derivation of the Green operator for strains).