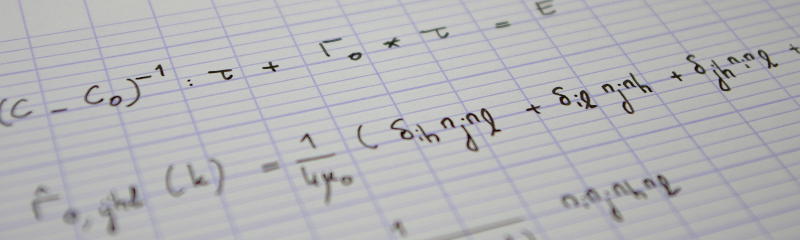In structural analysis, thick beams (resp. plates) usually refer to shear deformability, and the Timoshenko beam theory (resp. Mindlin–Reissner plate theory). With curved elements however (e.g. curved beams or shells), the situation is more subtle, as thickness corrections may be necessary even in shells where the shear stress is null at any point. In this series, this is illustrated with a spherical pressure vessel, for which the stress resultants and couples are studied. “Easy enough”, you probably think: $N=pR/2$, $M=0$ and that's the end of it (Wikipedia). Well, maybe…
In the first part of this series, Koiter's thin shell theory (Koiter, 1970, Actes du Congrès International des Mathématiciens, vol. 3, pp. 123–130) is used to analyse the equilibrium of the spherical pressure vessel. In particular, it is shown that the results deviate slightly from what is expected from the membrane theory.
Description of the problem
We consider a spherical vessel, subjected to an internal pressure $p$. $R$ denotes the radius of the midsurface, $h$ the thickness of the shell, so that the inner and outer radii of the shell are
$$R_\text{in}=R-\frac h2\quad\text{and}\quad R_\text{out}=R+\frac h2.$$
The problem is solved in spherical coordinates. From symmetry considerations (the problem is fully isotropic), the deflection $w$ (normal displacement of the midsurface) is constant. Similarly, the strain $\epsilon_{\alpha\beta}$, the change of curvature $\kappa_{\alpha\beta}$, the membrane force $N_{\alpha\beta}$ and the bending moment $M_{\alpha\beta}$ are all diagonal tensors with constant components
$$\epsilon_{\theta\theta}=\epsilon,\quad\epsilon_{\phi\phi}=\epsilon,\quad\epsilon_{\theta\phi}=0,\tag{1}$$
$$\kappa_{\theta\theta}=\kappa,\quad\kappa_{\phi\phi}=\kappa,\quad\kappa_{\theta\phi}=0,\tag{2}$$
$$N_{\theta\theta}=N,\quad N_{\phi\phi}=N,\quad N_{\theta\phi}=0,$$
$$M_{\theta\theta}=M,\quad M_{\phi\phi}=M,\quad M_{\theta\phi}=0,$$
where $\epsilon$, $\kappa$, $N$ and $M$ are four scalar constants, which will be determined in the next section by means of Koiter\'s linear theory of thin shells (Koiter, 1970).
The thin shell solution
Up to terms which are quadratic in the displacement, the trace of the tensor of membrane strains is equal to the relative variation of surface area of the shell. Therefore
$$\epsilon=\frac12\epsilon_{\alpha\alpha}=\frac12\frac{4\pi\bigl(R+w\bigr)^2-4\pi R^2}{4\pi R^2}\simeq\frac wR.\tag{3}$$
There is no simple geometrical derivation that I know of for the determination of the change of curvature, and you will have to trust me on this [… or use Eq. (3.4) in the paper by Koiter (1970)].
$$\kappa=-\frac w{R^2}.\tag{4}$$
The deflection $w$ of the shell is found by minimizing its total potential energy $\Pi=U-V$, where $U$ denotes the srain energy, and $V$ denotes the potential of external forces. In Koiter's theory of thin shells, the strain energy $U$ of the shell is the sum of two contributions: $U=U_\epsilon+U_\kappa$, with
$$U_\epsilon=\frac12\frac{Eh}{1-\nu^2}\int_{\Sigma}\bigl[\bigl(1-\nu\bigr)\epsilon_{\alpha\beta}\epsilon^{\alpha\beta}+\nu\bigl(\epsilon_\gamma^\gamma\bigr)^2\bigr]\mathrm{d}\Sigma=4\pi R^2\frac{Eh}{1-\nu}\epsilon^2,$$
$$U_\kappa=\frac12\frac{Eh^3}{12\bigl(1-\nu^2\bigr)}\int_{\Sigma}\bigl[\bigl(1-\nu\bigr)\kappa_{\alpha\beta}\kappa^{\alpha\beta}+\nu\bigl(\kappa_\gamma^\gamma\bigr)^2\bigr]\mathrm{d}\Sigma=4\pi R^2\frac{Eh^3}{12\bigl(1-\nu\bigr)}\kappa^2,$$
where use has been made of Eqs. (1) and (2). The strain energy of the shell therefore reads
$$U=4\pi R^2\frac{Eh}{1-\nu}\Bigl(1+\frac{h^2}{12R^2}\Bigr)\frac{w^2}{R^2},$$
while the potential of external loads $V$ is clearly given by the following expression
$$V=4\pi R^2 pw.$$
The total potential energy
$$\frac{\Pi}{4\pi R^2}=\frac{Eh}{1-\nu}\Bigl(1+\frac{h^2}{12R^2}\Bigr)\frac{w^2}{R^2}-pw$$
is then minimized with respect to the deflection $w$, which leads to
$$w=\frac{pR^2}{2Eh}\frac{1-\nu}{1+\frac{h^2}{12R^2}}.\tag{5}$$
The stress resultants and couples are then retrieved from the constitutive laws. For the stress resultants, we have
$$N=N_{\theta\theta}=\frac{Eh}{1-\nu^2}\bigl(\epsilon_{\theta\theta}+\nu\epsilon_{\phi\phi}\bigr)=\frac{Eh}{1-\nu^2}\bigl(1+\nu\bigr)\epsilon=\frac{Eh}{1-\nu}\epsilon,\tag{6}$$
and similarly for the stress couples
$$M=\frac{Eh^3}{12\bigl(1-\nu\bigr)}\kappa.\tag{7}$$
Substituting Eqs. (3), (4) and (5) in Eqs. (6) and (7) finally leads to the following expansions
$$N=\frac{pR}2\bigl(1-\frac{h^2}{12R^2}\bigr)+\mathcal O\bigl(\frac{h^4}{R^4}\bigr),$$ $$M=-\frac{ph^2}{24}\bigl(1-\frac{h^2}{12R^2}\bigr)+\mathcal O\bigl(\frac{h^6}{R^6}\bigr).$$
This is the first surprise in this series: the stress couple is not null, and the stress resultant differ slightly from the well-known formula $N=pR/2$ (see Wikipedia).
Nota: the above-mentioned formula $N=pR/2$ is known in french as “formule des chaudronniers”. One of my readers (Iliass Tahiri) kindly mentioned that it is known in english as Barlow's formula, referring to the mathematician Peter Barlow.
Conclusion
We started with a very simple shell, which we expected to be in a state of membrane equilibrium. However, using Koiter's linear theory of thin shells, we found that the stress couples, though small, are not null!
So what's wrong with the above analysis? To dig deeper into this problem, we will use its full 3D solution to compute exact values of the stress resultants and couples… which will lead to other exciting findings in the next instalment of this series!