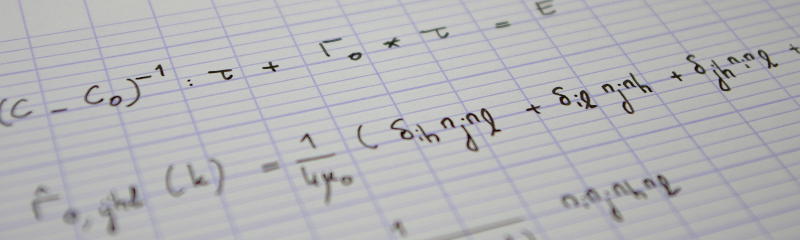My student Vinh Phuc Tran has recently had one of his papers published in Mechanics of Materials. The paper is called Stochastic modeling of mesoscopic elasticity random field. The abstract is reproduced below
In the homogenization setting, the effective properties of a heterogeneous material can be retrieved from the solution of the so-called corrector problem. In some cases of practical interest, obtaining such a solution remains a challenging computational task requiring an extremely fine discretization of microstructural features. In this context, Bignonnet et al. recently proposed a framework where smooth mesoscopic elasticity random fields are defined through a filtering procedure. In this work, we investigate the capabilities of information-theoretic random field models to accurately represent such mesoscopic elasticity fields. The aim is to substantially reduce the homogenization cost through the use of coarser discretizations while solving mesoscale corrector problems. The analysis is performed on a simple but non-trivial model microstructure. First of all, we recall the theoretical background related to the filtering and multiscale frameworks, and subsequently characterize some statistical properties of the filtered stiffness field. Based on these properties, we further introduce a random field model and address its calibration through statistical estimators and the maximum likelihood principle. Finally, the validation of the model is discussed by comparing some quantities of interest that are obtained either from numerical experiments on the underlying random microstructure or from model-based simulations. It is shown that for the case under study, the information-theoretic model can be calibrated with a limited set of realizations and still allows for accurate predictions of the effective properties.
This paper is available as a preprint on HAL ENPC. The published version is available here.