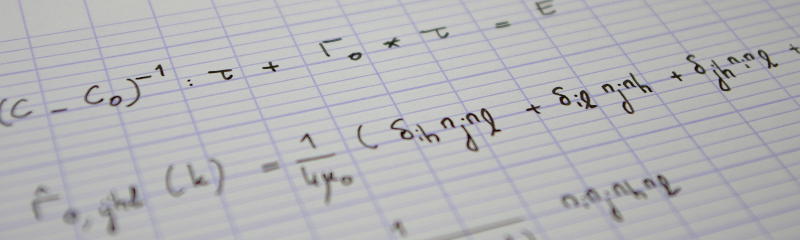My paper “Reconstructing displacements from the solution to the periodic Lippmann--Schwinger equation discretized on a uniform grid” has recently been published in International Journal of Numerical Methods in Engineering. The abstract is reproduced below
Uniform grid solvers of the periodic Lippmann--Schwinger equation have been introduced by Moulinec and Suquet for the numerical homogenization of heterogeneous materials. Based on the fast Fourier transform, these methods use the strain as main unknown and usually do not produce displacement fields. While this is generally not perceived as a restriction for homogenization purposes, some tasks might require kinematically admissible displacement fields.
In this paper, we show how the numerical solution to the periodic Lippmann--Schwinger equation can be post-processed to reconstruct a displacement field. Our procedure applies to any variant of the Moulinec--Suquet solver. The reconstruction is formulated as an auxiliary elastic equilibrium problem of a homogeneous material, which is solved with displacement-based finite elements. Taking advantage of periodicity, uniformity of the grid and homogeneity of the material, the resulting linear system is formulated and solved efficiently in Fourier space. The cost of our procedure is lower than that of one iteration of the Lippmann--Schwinger solver.
Two applications are proposed, in two and three dimensions. In the first application, the reconstructed displacement field is used to compute a rigorous upper bound on the effective shear modulus. In the second application, the quality of the reconstruction is assessed quantitatively.
This paper is available as a preprint on HAL ENPC. The published version is available here.