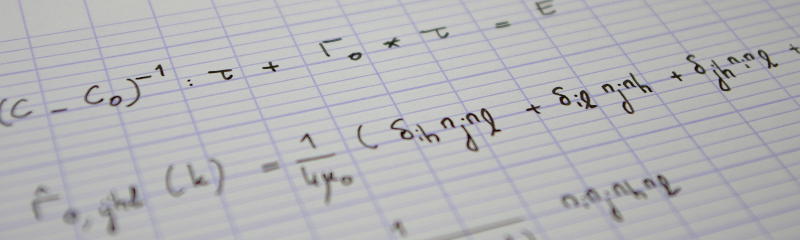My student Mohamed Hassan Khalili has recently had one of his papers published in Physical Review E. The paper is called “A numerical study of one-dimensional compression of granular materials”. I have only been very marginally involved in this DEM study, which is divided in two parts.
Part I is entitled “Stress-strain behavior, microstructure and irreversibility”. The abstract is reproduced below
The behavior of a model granular material, made of slightly polydisperse beads with Hertz-Mindlin elastic-frictional contacts, in oedometric compression (i.e., compression along one axis, with no lateral strain) is studied by grain-level numerical simulations. We systematically investigate the influence of the (idealized) packing process on the microstructure and stresses in the initial, weakly confined equilibrium state, and prepare both isotropic and anisotropic configurations differing in solid fraction Φ and coordination number z. Φ (ranging from maximally dense to moderately loose), z (which might vary independently of Φ in dense systems), fabric and force anisotropy parameters, and the ratio K₀ of lateral stresses σ₂=σ₃ to stress σ₁ in the compression direction are monitored in oedometric compression in which σ₁ varies by more than three orders of magnitude. K₀ reflects the anisotropy of the assembling process and may remain nearly constant in further loading if the material is already oedometrically compressed (as a granular gas) in the preparation stage. Otherwise, it tends to decrease steadily over the investigated stress range. It is related to force and fabric anisotropy parameters by a simple formula. Elastic moduli, separately computed with an appropriate matrix method, may express the response to very small stress increments about the transversely isotropic well-equilibrated states along the loading path, although oedometric compression proves an essentially anelastic process, mainly due to friction mobilization, with large irreversible effects apparent upon unloading. While the evolution of axial strain ε₁ and solid fraction Φ (or of the void ratio e=−1+1/Φ) with axial stress σ₁ is very nearly reversible, especially in dense samples, z is observed to decrease (as previously observed in isotropic compression) after a compression cycle if its initial value was high. K₀ relates to the evolution of internal variables and may exceed 1 in unloading. The considerably greater irreversibility of oedometric compression reported in sands, compared to our model systems, should signal contact plasticity or damage.
The preprint is available on HAL and the published version is available here.
Part II is entitled “Elastic moduli, stresses and microstructure”. The abstract is reproduced below
The elastic moduli of a transversely isotropic model granular material, made of slightly polydisperse elastic-frictional spherical beads, in equilibrium along a one-dimensional (oedometric) compression path, as described in the companion paper [M. H. Khalili et al., Phys. Rev. E 95, 032907 (2017)], are investigated by numerical simulations. The relations of the five independent moduli to stresses, density, coordination number, fabric and force anisotropies are studied for different internal material states along the oedometric loading path. It is observed that elastic moduli, as in isotropic packs, are primarily determined by the coordination number, with anomalously small shear moduli in poorly coordinated systems, whatever their density. Such states also exhibit faster increasing moduli in compression, and larger off-diagonal moduli and Poisson ratios. Anisotropy affects the longitudinal moduli C₁₁ in the axial direction and C₂₂ in the transverse directions, and the shear modulus in the transverse plane C₄₄, more than the shear modulus in a plane containing the axial direction C₅₅. The results are compared to available experiments on anisotropic bead packs, revealing, despite likely differences in internal states, a very similar range of stiffness level (linked to coordination), and semiquantitative agreement as regards the influence of anisotropy. Effective medium theory (the Voigt approach) provides quite inaccurate predictions of the moduli. It also significantly underestimates ratios C₁₁/C₂₂ (varying between 1 and 2.2) and C₅₅/C₄₄ (varying from 1 to 1.6), which characterize elastic anisotropy, except in relatively weakly anisotropic states. The bulk modulus for isotropic compression and the compliance corresponding to stress increments proportional to the previous stress values are the only elastic coefficients to be correctly estimated by available predictive relations. We discuss the influences of fabric and force anisotropies onto elastic anisotropy, showing in particular that the former dominates in sample series that are directly assembled in anisotropic configurations and keep a roughly constant lateral to axial stress ratio under compression.
See the preprint on HAL and the published version.