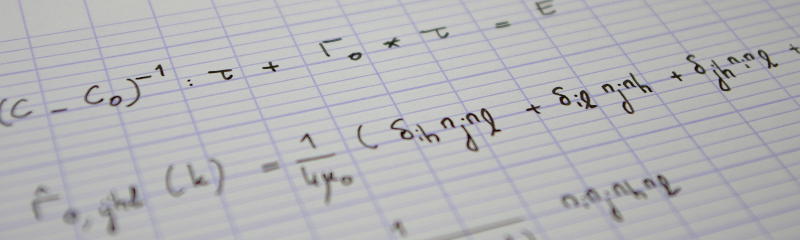On monday 20th, november 2017 (at 13:30), I will be defending my "Habilitation à Diriger des Recherches" at École des Ponts ParisTech in front of the following jury
- Renald Brenner (Sorbonne Universités, UPMC Univ Paris 06, CNRS, UMR 7190, Institut Jean le Rond d\'Alembert, F-75005, Paris, France),
- Samuel Forest (Centre des Matériaux, Mines ParisTech, UMR CNRS 7633, BP 87, Évry Cedex, France),
- Pierre Gilormini (Laboratoire PIMM, ENSAM, CNRS, CNAM, 151 bd de l'Hôpital, 75013 Paris, France),
- Christian Hellmich (Institute for Mechanics of Materials and Structures, TU Wien–Vienna Univ. of Technology, Karlsplatz 13/202, A-1040 Vienna, Austria),
- Patrick Le Tallec (Laboratoire de Mécanique des Solides, École Polytechnique, Route de Saclay, 91128 Palaiseau, France),
- Karam Sab (Université Paris-Est, Laboratoire Navier, ENPC, IFSTTAR, CNRS UMR 8205, 6-8 Avenue Blaise Pascal, Cité Descartes, 77455 Marne-la Vallée, France).
The abstract of my habilitation report is reproduced below
The present report is submitted in partial fulfilment of the French habilitation degree (Habilitation à Diriger des Recherches). Covering the period 2011–2017, it gives an overview of a selection of my research activities, conducted essentially at Laboratoire Navier.
Most of my research has been devoted to understanding how the macroscopic properties of random, heterogeneous materials relate to their microstructure. To investigate this question, I used almost systematically a variational approach based on the Hashin–Shtrikman principle, which results in a fairly consistent report. The reason for selecting such a tool lies in its high versatility; indeed, any trial field is admissible. This is extremely valuable for highly heterogeneous materials, where it can be difficult to propose e.g. admissible stress or strain fields.
The Hashin–Shtrikman principle is applied here in two different situations: i. in a statistical (theoretical) setting, and ii. in a numerical setting relying on Galerkin discretizations. In the former situation, the Hashin–Shtrikman principle leads to closed-form (or at least, semi-analytical) bounds or estimates of the effective properties. In the latter situation, the Hashin–Shtrikman principle allows to revisit a few existing full-field techniques. My contributions in both areas are discussed in two separate chapters.
For the sake of consistency of the present document, some of my research activities (relating to X-ray tomography and image analysis) have been purposely discarded. They are briefly discussed in the last chapter as a part of my prospective research project.
The manuscript is available on the HAL platform.