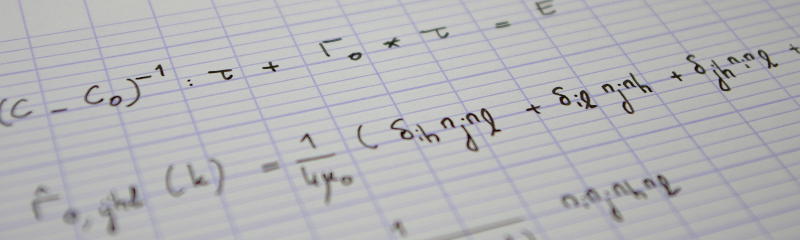Most of my research activities deal with upscaling the mechanical properties of heterogeneous materials. This is also known as homogenization. So what is homogenization? This series explores this question; it is largely based on the introduction to my Habilitation defense.
In order to introduce homogenization, we will draw inspiration from the publishing industry. The following photograph1 was published in Le Journal (a french daily newspaper) from thursday, may 30th, 1935. It illustrates the first cruise of the ocean liner Normandie.

From where you sit, water exhibits nice shades of gray. However, let us take a closer look at the prow:

It turns out that the sea has a dotted structure, which is inherent to the so-called halftoning technique itself. Of course, the reason why the resulting picture looks fine is because you are looking at it from far off. Also, the size of the “gray” patches must be large enough for you to get the illusion that it is smoothly shaded. Indeed, if the patch contains only a few dots, the illusion will not take place.
We have therefore identified three length-scales
- the microscopic length-scale $L_\mu$ is the size of the dots,
- the mesoscopic length-scale $L_{\mathrm{m}}$ is the typical size of the patches,
- the macroscopic length-scale $L_{\mathrm{M}}$ is the distance from your screen to your eye.
These three scales must be well separated for the photograph to appear smoothly shaded. In other words, the macro scale is much larger than the meso scale, which in turn is much larger than the micro scale: $L_{\mu} \ll L_{\mathrm{m}} \ll L_{\mathrm{M}}$. This is the so-called assumption of separation of scales.
Provided that separation of scales prevails, homogenization can take place. Homogenization is the process of replacing the complex microstructure with an equivalent, homogeneous mesostructure. By microstructure, we mean both the geometry and physical properties of the microscopic features. In the above example, the microstructure is defined by the size and spacing of the dots (geometry), as well as the color of dots and background (physical properties). The mesostructure on the other hand is a patch with homogeneous, equivalent (in homogenization language, we say effective) properties. In the above example, the effective property is the shade of gray as perceived by the observer.
Conclusion
In this post, we introduced the homogenization concept through a graphical analogy. We explained that the key ingredient for homogenization to be valid is separation of scales.
In the next instalment of this series, we will discuss two strategies to carry out homogenization: the bottom-up and top-down approaches.