This post is not going to be the most exciting I have ever written. We will derive the expression of the elastic energy of a linear spring as a function of the displacement of its two end-points. I will need this expression in my series on “What is homogenization”. Having derived the elastic energy, we will be only one step away from the stiffness matrix of the spring, to be used in a finite element setting.
Expression of the elastic energy
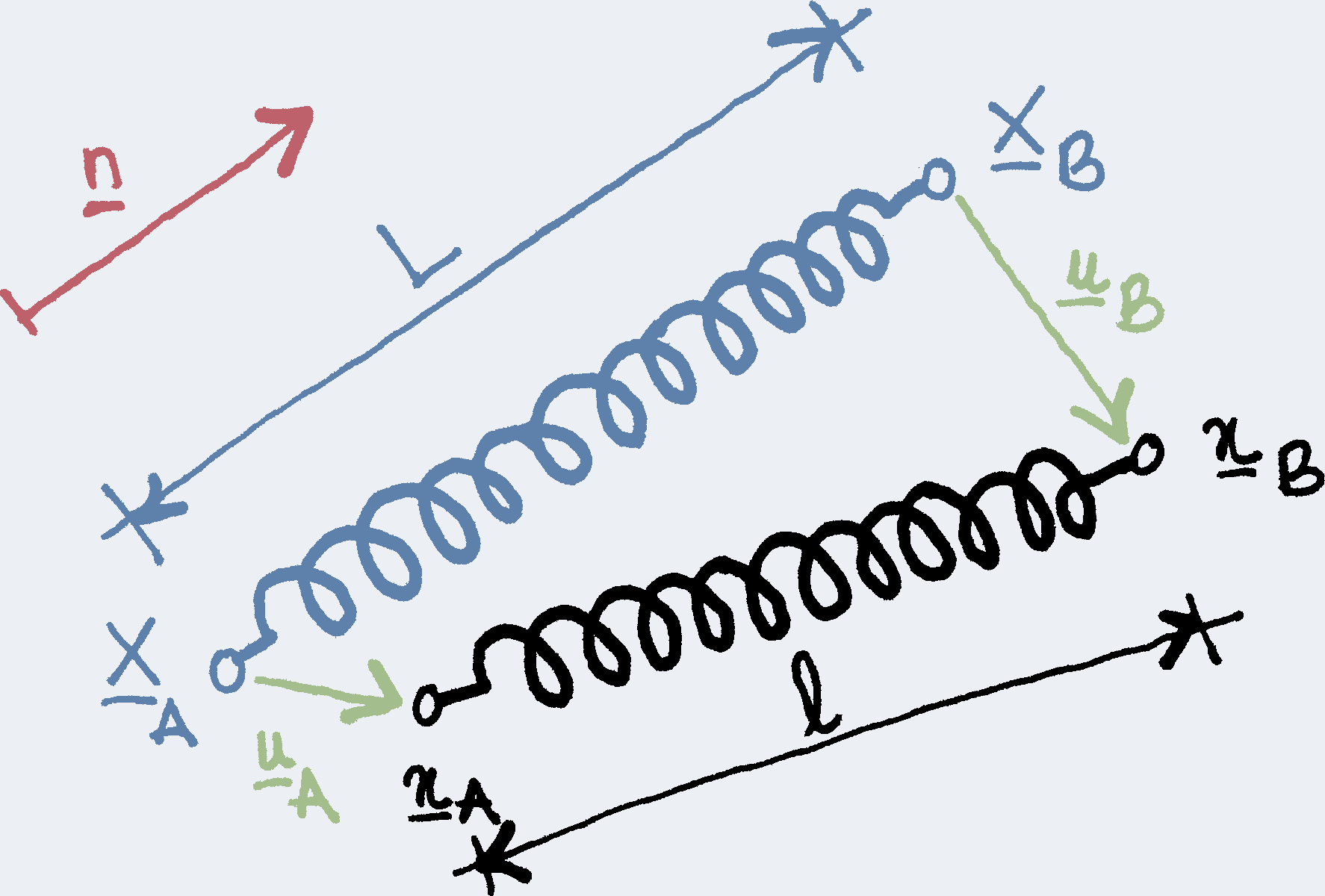
We consider a spring located between points $A$ and $B$. Its initial length (at rest) is $L$, and we introduce the unit vector $\vec n$ that points from $A$ to $B$
$$\vec X_B=\vec X_A+L\,\vec n,$$
where $\vec X_A$ and $\vec X_B$ denote the radius vectors of points $A$ and $B$ in the initial (undeformed) configuration.
At equilibrium, the length of the spring is $\ell$ and its elastic energy is $$U=\tfrac12k\bigl(\ell-L\bigr)^2,$$ where $k$ denotes the stiffness of the spring. We want to express this elastic energy as a function of the displacements $\vec u_A$ and $\vec u_B$ of the points $A$ and $B$
$$\vec x_A=\vec X_A+\vec u_A\quad\text{and}\quad\vec x_B=\vec X_B+\vec u_B,$$
where $\vec x_A$ and $\vec x_B$ now denote the radius vectors of points $A$ and $B$ in the current (deformed) configuration. We will work under the assumption that these displacements are small and we will keep only the lowest order term of the energy.
We have
$$\ell=\lVert\vec x_B-\vec x_A\rVert=\lVert\vec X_B-\vec X_A+\vec u_B-\vec u_A\rVert=L\lVert\vec n+\vec\xi\rVert,$$
where we have introduced the following dimensionless vector
$$\vec\xi=L^{-1}\bigl(\vec u_B-\vec u_A\bigr).$$
Then
$$\ell^2=L^2\bigl(\vec n+\vec\xi\bigr)^2=L^2\bigl(1+2\,\vec n\cdot\vec\xi+\vec\xi\cdot\vec\xi\bigr)$$
and, to first order in $\vec\xi$
$$\ell=L\bigl[1+\vec n\cdot\vec\xi+\mathcal O(\vec\xi^2)\bigr].$$
Plugging the expression of $\vec\xi$ as a function of the displacements $\vec u_A$ and $\vec u_B$, we find the elongation of the spring
$$\ell-L=\vec n\cdot\bigl(\vec u_B-\vec u_A\bigr)+\text{h.o.t.}$$
Finally, the elastic energy of the spring is, to lowest order
$$U=\tfrac12k\bigl[\vec n\cdot\bigl(\vec u_B-\vec u_A\bigr)\bigr]^2,$$
which is the expression we were looking for.
Expression of the stiffness matrix
The above expression can also be written
$$U=\tfrac12k\bigl(\vec u_B-\vec u_A\bigr)\cdot\bigl(\vec n\otimes\vec n\bigr)\cdot\bigl(\vec u_B-\vec u_A\bigr)$$
and, upon expansion
$$U=\tfrac12k\bigl[\vec u_A\cdot\bigl(\vec n\otimes\vec n\bigr)\cdot\vec u_A+\vec u_B\cdot\bigl(\vec n\otimes\vec n\bigr)\cdot\vec u_B-2\vec u_A\cdot\bigl(\vec n\otimes\vec n\bigr)\cdot\vec u_B\bigr].$$
This delivers the expression of the stiffness matrix of the spring. Indeed, let $q$ be the vector of dofs of the spring. This is a column vector of size $2d$ ($d$: number of spatial dimensions): $q=[\vec u_A, \vec u_B]^\mathsf{T}$, where we store first the $d$ components of the displacement of point $A$, then the $d$ components of the displacement of point $B$. The elastic energy of the spring can now be written
$$U=\tfrac12q^\mathsf{T}\cdot K\cdot q,$$
where the stiffness matrix $K$ reads, in block form
$$K=k\begin{bmatrix}\vec n\otimes\vec n & -\vec n\otimes\vec n\\-\vec n\otimes\vec n & \vec n\otimes\vec n\end{bmatrix}.$$
For $d=2$, we introduce the components $u_\star$ and $v_\star$ of the displacement $\vec u_\star$
$$\vec u_\star=u_\star\,\vec e_x+v_\star\,\vec e_y,\quad q^\mathsf{T}=\bigl[u_A, v_A, u_B, v_B\bigr]$$
and
$$K=k\begin{bmatrix} n_xn_x & n_xn_y & -n_xn_x & -n_xn_y\\ n_xn_y & n_yn_y & -n_xn_y & -n_yn_y\\ -n_xn_x & -n_xn_y & n_xn_x & n_xn_y\\ -n_xn_y & -n_yn_y & n_xn_y & n_yn_y \end{bmatrix}.$$
For $d=3$, we introduce the components $u_\star$, $v_\star$ and $w_\star$ of the displacement $\vec u_\star$
$$\vec u_\star=u_\star\,\vec e_x+v_\star\,\vec e_y+w_\star\,\vec e_z,\quad q^\mathsf{T}=\bigl[u_A, v_A, w_A, u_B, v_B, w_B\bigr]$$
and
$$K=k\begin{bmatrix} n_xn_x & n_xn_y & n_xn_z & -n_xn_x & -n_xn_y & -n_xn_z\\ n_yn_x & n_yn_y & n_yn_z & -n_yn_x & -n_yn_y & -n_yn_z\\ n_zn_x & n_zn_y & n_zn_z & -n_zn_x & -n_zn_y & -n_zn_z\\ -n_xn_x & -n_xn_y & -n_xn_z & n_xn_x & n_xn_y & n_xn_z\\ -n_yn_x & -n_yn_y & -n_yn_z & n_yn_x & n_yn_y & n_yn_z\\ -n_zn_x & -n_zn_y & -n_zn_z & n_zn_x & n_zn_y & n_zn_z \end{bmatrix}.$$