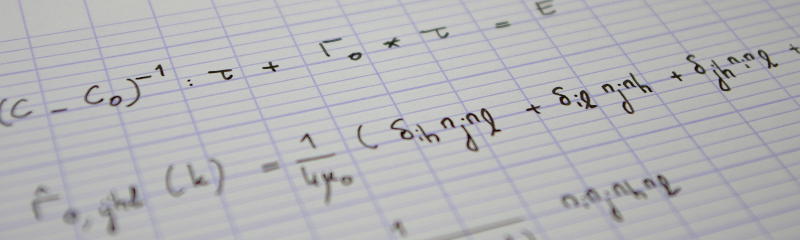Finding the stress resultant and stress couple in a spherical pressure vessel seems easy enough. Well, this apparently simple problem allows us to highlight subtle thickness effects within shells. It should be emphasized again that these thickness effects have nothing to do with shear corrections. Indeed, shear stresses are null at any point of the spherical pressure vessel. Rather, the thickness effects we are discussing in this series are due to curvature.
In the first instalment of this series, I showed that using Koiter's thin shell solution leads to a non-null stress couple, which came as quite a surprise. In the second instalment, I used the exact, 3D solution to derive reference values of the stress couple and stress resultant through integration over the thickness of the shell. In particular, I showed that thickness corrections had to be incorporated.
This still does not settle the matter, since the results obtained within the framework of Koiter's thin shell theory (see first instalment) are inconsistent with the reference, 3D elasticity values (see second instalment). To reconcile both approaches (3D elasticity vs. shell theory), we need to use a thick shell theory, as illustrated below.
Strain distribution in the spherical pressure vessel
The fundamental assumption of all shell theories is that displacement of any point of the shell is completely defined by the rigid body motion (translation and rotation) of its projection onto the base surface. In the present case, owing to the symmetries of the problem, points of the base surface move along the normal $\mathbf n$
$$\mathbf u = w\mathbf n,\tag{1}$$
where $w$ is the normal displacement, which is constant over the base surface. Since the rotation is null, all points (across the thickness of the shell) have the same normal displacement. Therefore, Eq. (1) defines the 3D displacement field within the shell, seen as a 3D continuum. From this 3D displacement field, we can readily derive the corresponding strain field. We will use a simplified, geometric approach, rather than the general formulas in spherical coordinates. This is possible because there are so many symmetries in the problem at hand!
The in-plane strain $\epsilon$ at the distance $r$ of the center is given by the relative change of length of the equator
$$\epsilon=\frac{2\pi\bigl(r+w\bigr)-2\pi r}{2\pi r}=\frac wr.\tag{2}$$
In the first instalment, we found $\epsilon=w/R$, where $R$ is the radius of the midsurface. Eq. (2) therefore incorporates thickness corrections which we previously overlooked.
Stress distribution in the spherical pressure vessel
Stresses in the spherical pressure vessel are derived from the strains [see Eq. (2)], within the framework of plane stress elasticity
$$\sigma_{\theta\theta}=\frac E{1-\nu^2}\bigl(\epsilon_{\theta\theta}+\nu\epsilon_{\phi\phi}\bigr)\tag{3}$$
$$\sigma_{\phi\phi}=\frac E{1-\nu^2}\bigl(\epsilon_{\phi\phi}+\nu\epsilon_{\theta\theta}\bigr).\tag{4}$$
Since the solution is isotropic ($\epsilon_{\theta\theta}=\epsilon_{\phi\phi}=\epsilon$ and $\sigma_{\theta\theta}=\sigma_{\phi\phi}=\sigma$), Eqs. (3) and (4) lead to
$$\sigma=\frac E{1-\nu}\epsilon=\frac E{1-\nu}\frac wr.\tag{5}$$
Stress resultant and stress couple
Eq. (5) is finally integrated over the thickness of the shell to obtain the stress resultant and stress couple. Integration must include thickness corrections, which amount to a $r/R$ factor within the integral (see previous instalment of this series).
$$N=\int_{R_\mathrm{int}}^{R_\mathrm{ext}}\sigma(r)\,\frac rR\,\mathrm{d}r=\frac{Eh}{1-\nu}\frac wR,\tag{6}$$
$$M=\int_{R_\mathrm{int}}^{R_\mathrm{ext}}-\bigl(r-R\bigr)\sigma(r)\,\frac rR\,\mathrm{d}r=0.\tag{7}$$
Now, things start getting really interesting! Indeed, in the thick shell approach, the stress couple is (as expected) rigorously null! Since $M=0$, it can readily be deduced that
In other words, the classical formula is retrieved (see Wikipedia).
Conclusion
In the present post, we finally resolved all contradictions regarding the computation of stress resultant and stress couple within a spherical pressure vessel. In the discussion below, $\eta$ denotes the slenderness of the shell, $\eta=h/R$. Besides, by “k-th order terms”, we mean terms of order $\eta^k$.
Four difference approaches can be followed to analyse the equilibrium of a spherical pressure vessel (see table below). In the classical membrane approach, stress couples are overlooked, and the classical formula $N=pR/2$ is obtained.
In the thin shell approach, the stress resultant deviates slightly from this classical value (by second order terms) and the stress couple is not null (rather, it is of second order).
In the thick shell approach, the stress couple is rigorously null and the classical formula is retrieved for the stress resultant. Thickness corrections appear in two different places
- in the strain distribution across the thickness of the shell [see Eq. (2)]: the distribution is hyperbolic with respect to the thickness coordinate,
- in the stress-stress resultant and stress-stress couple integral relations [see Eqs. (6) and (7)].
In the 3D approach, the true stress resultant differs from $N=pR/2$ by second order terms, while the true stress couple is of fourth order.
What should we deduce from this study? Obviously, beware thin shell theories! Fortunately, I believe that most FE codes implement the thick shell theory. More fundamentally, I am still trying to understand what these results really imply. Does that mean that the asymptotic convergence (as the thickness tends to zero) of thick shell models is faster than that of thin shell models? That is something I am going to investigate.
This closes our series on thick shells. I hope you enjoyed reading it… and maybe learned something! Should you want to dig deeper into various thick shell theories, do start with Leissa (1973), who gives a good overview.
| Exact 3D theory | Thin shell theory | Thick shell theory | |
|---|---|---|---|
| Stress resultant (deviation from pR/2) | η² | η² | 0 |
| Stress couple | η⁴ | η² | 0 |