In this post, we compute numeric values of the apparent stiffness introduced in this post. Our goal is to find the solution to the general problem depicted below.
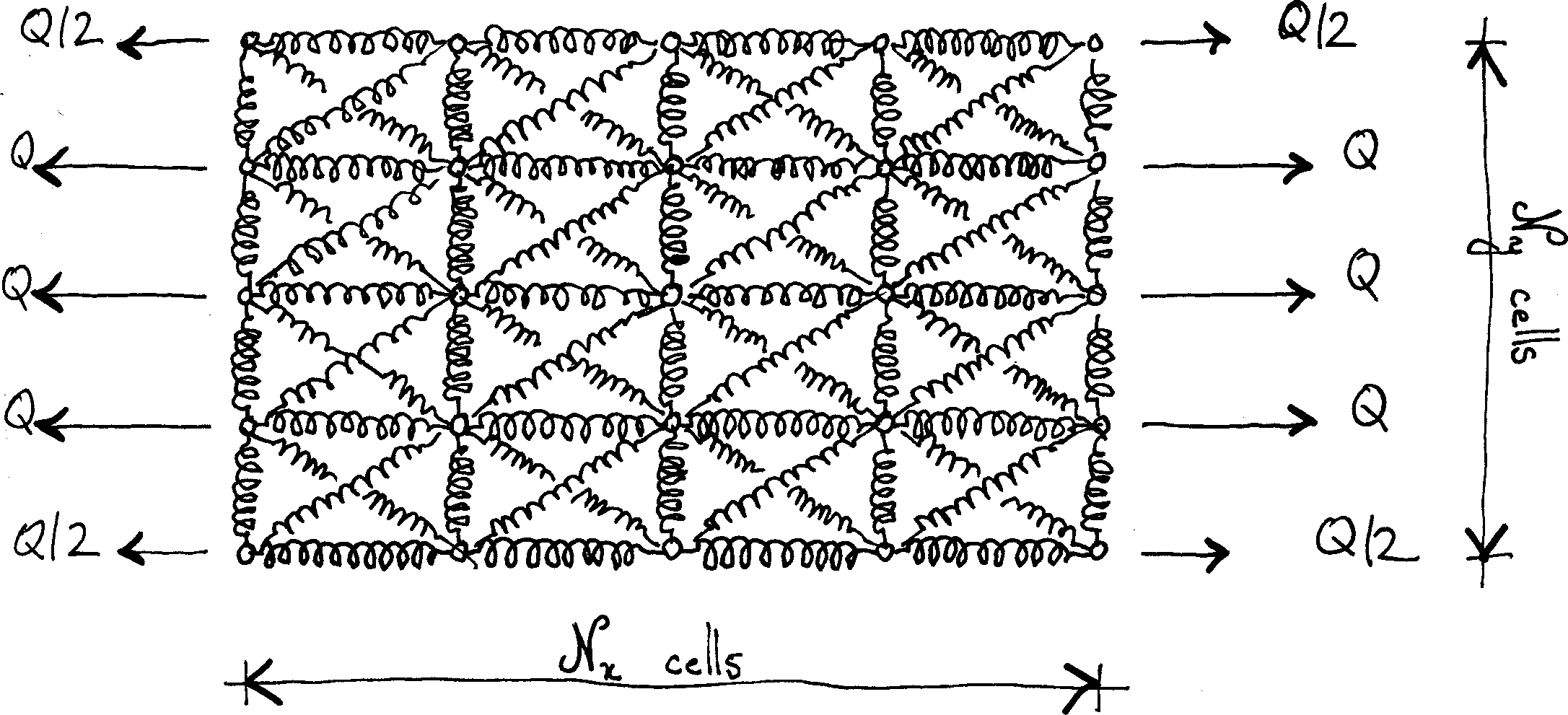
We use a numeric approach that is akin to the finite element method. More precisely, we minimize the total potential energy of the spring with respect to the nodal displacements.
This time, we will use the Julia programming language.
using DelimitedFiles
using LinearAlgebra
using Plots
using Test
We first define a function that returns the stiffness matrix ox a single spring, according to this post.
"""spring_stiffness_matrix(k, nx, ny)
Return the stiffness matrix of the spring with stiffness `k` and direction `(nx, ny)`.
The direction must be a unit vector (`nx² + ny² == 1`).
The degrees of freedom of the spring are ordered as follows:
1. horizontal displacement of node 1,
2. vertical displacement of node 1,
3. horizontal displacement of node 2,
4. vertical displacement of node 2.
"""
function spring_stiffness_matrix(k, nx, ny)
kxx = k * nx * nx
kyy = k * ny * ny
kxy = k * nx * ny
return [
kxx kxy -kxx -kxy;
kxy kyy -kxy -kyy;
-kxx -kxy kxx kxy;
-kxy -kyy kxy kyy]
end
spring_stiffness_matrix
We then define a structure that holds the description of the mesh. See this post for a description of the various symbols. Note that for the sake of simplicity, it is assumed that the number of cells is identical in both directions.
struct SpringMesh
χx::Float64
χy::Float64
θ::Float64
ncells::Int
ndofs::Int
SpringMesh(χx, χy, θ, ncells) = new(χx, χy, θ, ncells, 2 * (ncells+1)^2)
end
We define a function that computes the linear index of the node located at (i⋅Δx, j⋅Δy). It would probably have been better to use CartesianIndices for this purpose.
"""node_at(i, j, mesh)
Return the linear indnex of the node located at `(i, j)` in the mesh.
Note that `i` and `j` are zero-based, while the returned index in one-based.
"""
function node_at(i, j, mesh)
(mesh.ncells+1)*j+i+1
end
node_at
To assemble the global stiffness matrix, we add block-wise the element stiffness matrix of each spring.
"""
add_spring_stiffness_matrix!(K, i1, j1, i2, j2, mesh, Ke)
Add to the global stiffness matrix `K` the element stiffness matrix `Ke`.
The spring connects nodes `(i1, j1)` and `(i2, j2)` (0-based indices).
"""
function add_spring_stiffness_matrix!(K, i1, j1, i2, j2, mesh, Ke)
n1 = node_at(i1, j1, mesh)
n2 = node_at(i2, j2, mesh)
index = [2n1-1, 2n1, 2n2-1, 2n2]
for i = 1:4
for j = 1:4
K[index[i], index[j]] += Ke[i, j]
end
end
end
add_spring_stiffness_matrix!
"""Return the stiffness matrix"""
function global_stiffness_matrix(mesh)
K = zeros(mesh.ndofs, mesh.ndofs)
c = cos(mesh.θ)
s = sin(mesh.θ)
K_h = spring_stiffness_matrix(mesh.χx, 1., 0.)
K_v = spring_stiffness_matrix(mesh.χy, 0., 1.)
K_d1 = spring_stiffness_matrix(1., c, s)
K_d2 = spring_stiffness_matrix(1., -c, s)
for i = 0:mesh.ncells
for j = 0:mesh.ncells
if i < mesh.ncells
add_spring_stiffness_matrix!(K, i, j, i + 1, j, mesh, K_h)
end
if j < mesh.ncells
add_spring_stiffness_matrix!(K, i, j, i, j + 1, mesh, K_v)
end
if (i < mesh.ncells) && (j < mesh.ncells)
add_spring_stiffness_matrix!(K, i, j, i + 1, j + 1, mesh, K_d1)
add_spring_stiffness_matrix!(K, i + 1, j, i, j + 1, mesh, K_d2)
end
end
end
return K
end
global_stiffness_matrix
The forces are applied only on the left and right boundaries. Assembly of the vector of nodal forces is done below.
"""nodal_forces(mesh)
Return the vector of nodal forces.
The total force applied on each side is 1.
"""
function nodal_forces(mesh)
F = zeros(mesh.ndofs)
f = 1. / mesh.ncells
for j=1:mesh.ncells-1
F[2 * node_at(0, j, mesh)-1] = -f
F[2 * node_at(mesh.ncells, j, mesh)-1] = f
end
F[2 * node_at(0, 0, mesh)-1] = -0.5 * f
F[2 * node_at(0, mesh.ncells, mesh)-1] = -0.5 * f
F[2 * node_at(mesh.ncells, 0, mesh)-1] = 0.5 * f
F[2 * node_at(mesh.ncells, mesh.ncells, mesh)-1] = 0.5 * f
return F
end
nodal_forces
We need to account for the boundary conditions that will prevent rigid body motion. We first define a general function that modifies the linear system to account for a fixed dof.
"""apply_bc!(K, F, fixed_dof, mesh)
Modify the stiffness matrix and vector of nodal forces to account for a fixed dof.
"""
function apply_bc!(K, F, fixed_dof, mesh)
for dof = 1:mesh.ndofs
K[fixed_dof, dof] = 0.
K[dof, fixed_dof] = 0.
end
K[fixed_dof, fixed_dof] = 1.
F[fixed_dof] = 0.
end
apply_bc!
The above function is then used to pin the lower-left corner and prevent vertical displacements of the lower-right corner as well as horizontal displacements of the upper-left corner.
function apply_bcs!(K, F, mesh)
n0 = node_at(0, 0, mesh)
apply_bc!(K, F, 2n0-1, mesh)
apply_bc!(K, F, 2n0, mesh)
n1 = node_at(mesh.ncells, 0, mesh)
apply_bc!(K, F, 2n1, mesh)
n2 = node_at(0, mesh.ncells, mesh)
apply_bc!(K, F, 2n2-1, mesh)
end
apply_bcs! (generic function with 1 method)
Finally, the apparent stiffness is computed according to this post.
function apparent_stiffness(mesh)
K = global_stiffness_matrix(mesh)
F = nodal_forces(mesh)
apply_bcs!(K, F, mesh)
u = K\F
elongation = 0.
for j = 0:mesh.ncells
left = 2 * node_at(0, j, mesh)-1
right = 2 * node_at(mesh.ncells, j, mesh)-1
weight = (j == 0) || (j == mesh.ncells) ? 0.5 : 1.0
elongation += weight * (u[right] - u[left])
end
elongation /= mesh.ncells
return 1. / elongation
end
apparent_stiffness (generic function with 1 method)
We use the symbolic expressions derived in this post to test our implementation.
actual_stiffness(χ, n) = apparent_stiffness(SpringMesh(χ, χ, π/4, n))
effective_stiffness(χ) = χ*(χ+2)/(χ+1)
expected_stiffness_1x1(χ) = 4χ*(χ+1)/(2χ+1)
expected_stiffness_2x2(χ) = 8χ*(1+χ)*(2+χ)/(2χ+3)/(3χ+2)
expected_stiffness_3x3(χ) = 144χ*(χ+1)*(4*χ^4+24χ^3+41χ^2+24χ+4)/(480χ^5+2888χ^4+5616χ^3+4771χ^2+1800χ+236)
@testset "Apparent stiffness" begin
χ = 2.0 .^ LinRange(-7, 7, 13)
@test actual_stiffness.(χ, 1) ≈ expected_stiffness_1x1.(χ)
@test actual_stiffness.(χ, 2) ≈ expected_stiffness_2x2.(χ)
@test actual_stiffness.(χ, 3) ≈ expected_stiffness_3x3.(χ)
end;
[37m[1mTest Summary: | [22m[39m[32m[1mPass [22m[39m[36m[1mTotal[22m[39m
Apparent stiffness | [32m 3 [39m[36m 3[39m
We then are ready to produce the figures that were used in this post.
χ = 2.
χx = χ
χy = χ
θ = π / 4.
npoints = 8
ncells = 1 .<< (0:(npoints-1))
A_app = zeros(npoints)
for i = 1:npoints
print("$(ncells[i]), ")
mesh = SpringMesh(χx, χy, θ, ncells[i])
A_app[i] = apparent_stiffness(mesh)
println(A_app[i])
end
1, 4.8
2, 3.4285714285714284
4, 3.0300228871509
8, 2.8619379280855037
16, 2.7748131542266377
32, 2.72562591606945
64, 2.698019760598084
128, 2.6829903494073495
Ax = cot(θ)*(1+cos(2θ)+χx)
Ay = tan(θ)*(1-cos(2θ)+χy)
Axy = sin(2θ)
A_eff = Ax - Axy^2 / Ay
2.6666666666666674
err = (A_app[:] .- A_eff) / A_eff
plot(ncells, 100*err,
axis=:log,
marker=:circle,
label="",
xlabel="Number of cells",
ylabel="Relative error [%]",
title="Relative error on effective stiffness")
basename = "apparent_stiffness_vs_number_of_cells"
savefig(basename * ".png")
# savefig(basename * ".pdf")
open(basename * ".csv", "w") do io
write(io, "# Apparent, uniaxial stiffness vs. number of cells\n")
write(io, "# chi_x = $χx\n")
write(io, "# chi_y = $χy\n")
write(io, "# theta = $θ rad\n")
writedlm(io, [ncells A_app], ",")
end
χ = 10.0 .^ LinRange(-2, 2, 41)
eff = effective_stiffness.(χ)
plot(χ, (expected_stiffness_1x1.(χ).-eff)./eff,
label="1×1",
xaxis=:log,
xlabel="Stiffness ratio, χ",
ylabel="Relative error")
plot!(χ, (expected_stiffness_2x2.(χ).-eff)./eff,
label="2×2",
xaxis=:log)
plot!(χ, (expected_stiffness_3x3.(χ).-eff)./eff,
label="3×3",
xaxis=:log)
basename = "apparent_stiffness_vs_chi"
savefig(basename * ".png")
# savefig(basename * ".pdf")