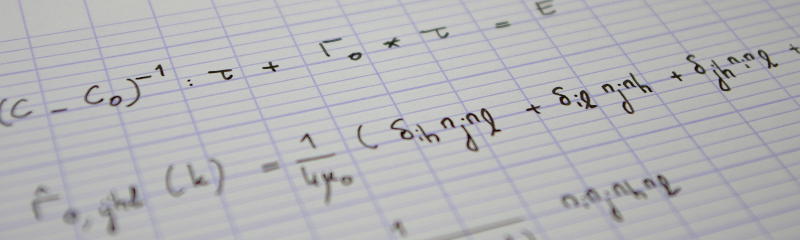Orientation correlations among rice grains, part 4: defining the ROI

In the previous instalment of this series, we obtained binned slices of the sample. Fig. 1 below displays a typical example of these binned slices. We now want to segment the rice grains. However, the analysis (in particular, Otsu thresholding) might be perturbed by the fact that the walls of the sample container are visible on the 3D image. In this post, I will show how we can locate these walls. Then, any subsequent analysis will be performed within the Region Of Interest (ROI) thus defined.

The circle Hough Transform

The sample container is cylindrical; since it was nearly vertical during the tomography experiment, its trace is a circular ring on each slice. We are going to use the Circle Hough Transform in order to locate the inner and outer circular boundaries which define this ring. To do so, we will use python, numpy and scikit-image. We first import these modules, and load the image

import os.path

import numpy as np

from skimage.color import gray2rgb
from skimage.draw import circle_perimeter
from skimage.feature import canny
from skimage.io import imread, imsave
from skimage.transform import hough_circle
from skimage.util import img_as_ubyte

root = '.'
name = os.path.join(root, 'rice-bin_4x4x4-099.tif')
img = imread(name)

print('Read {}x{} image.'.format(*img.shape))

Read 437x436 image.

Then, we locate the edges, by means of a standard Canny edge detector (see also the API docs of scikit-image).

edges = canny(img, sigma=0.)
imsave(os.path.join(root, 'rice-bin_4x4x4-edges-099.png'),
       img_as_ubyte(edges))

The resulting image is shown in Fig. 2. It should be noted that due to the preliminary binning (which is nothing but a mean filter), the input image exhibits very little noise. Therefore, sigma=0.0 in the above call to skimage.feature.canny.

We are now ready to compute the Circle Hough Transform. This transform aims at finding circles within an image. It was proposed by Duda and Hart (1971) (see also Wikipedia). It should be understood as a histogram in parameter space. More precisely, a point $(x, y)$ belongs to the circle centered at $(c_x, c_y)$ and of radius $r$ if, and only if

$$(x-c_x)^2+(y-c_y)^2=r^2.$$

The circle under consideration is parameterized by $(c_x, c_y, r)$. Conversely, given a point $(x, y)$, the set of circles to which this point belongs is given by the triplet $(c_x, c_y, r)$ such that

$$(c_x-x)^2+(c_y-y)^2-r^2=0.$$

In the parameter space $(c_x, c_y, r)$, the set of circles to which point $(x, y)$ belongs is a conical surface. Its apex is $(x, y, 0)$, its axis is the $(0, 0, 1)$ direction and its aperture is 90°. As we are only interested in real circles, only the $r\geq0$ half-space should be considered.

How is this representation in parameter space to be used? We consider a binary (0/1) image; let ${(x_i, y_i),i=1,\ldots,N}$ denote the set of non-null pixels. We define $\mathcal H_i$ as the 3D, binary image of the cone associated in the sphere parameter space with pixel $(x_i, y_i)$. The Hough transform is then the (possibly normalized) sum of all $\mathcal H_i$

$$\mathcal H(c_x, c_y, r)=\sum_i\mathcal H_i(c_x, c_y, r).$$

$\mathcal H$ should really be understood as a histogram. Indeed, a peak in $\mathcal H$ indicates that the cones corresponding to many pixels intersect at the same point in parameter space. In other words, many pixels in the original image belong to the same circle. Finding circles in the original image therefore reduces to finding peaks in its Hough transform. That is what we are going to do presently. We must first compute the Hough transform. In order to reduce the CPU cost, we will only consider these circles whose radius is close to that of the sample container. We saw in part 2 of this series that the radius of the sample container is 25 mm, while the voxel size is approximately 0.03 mm; after binning, the voxel size is therefore 0.12 mm, and the radius of the sample container is approx. 25 / 0.12 = 208 px. In the following code, we ask for the circle Hough transform for circles with radii between 190 and 220 px.

We first tell Python to ignore all warnings. This is extremely poor practice, but otherwise skimage.io.imsave will complain about low-contrast images (and my version of skimage does not implement the check_contrast keyword argument).

import warnings
warnings.filterwarnings("ignore")

radii = np.arange(190, 220)
h = hough_circle(edges, radii)
for i, radius in enumerate(radii):
    imsave(os.path.join(root,
                        'rice-bin_4x4x4-hough-099-{}.tif'.format(radius)),
           h[i, ...])

The above code snippet saves a series of images, which is displayed below in 3D as an animated GIF (see Fig. 3). The two bright spots indicate the location of the inner and outer boundaries in the parameter space. We will use a very crude procedure to locate these two peaks (a more elaborate method is not required as we do not seek sub-pixel accuracy).

The code snippet below finds the two highest values of the Hough transform. The correct peak (inner boundary) corresponds to the smallest radius. Then, the coordinates of the center of the corresponding circle are found.

h_max = np.max(h, axis=(1, 2))
k = np.min(np.argsort(h_max)[-2:])
radius = radii[k]
h = h[k, ...]
row, col = np.unravel_index(np.argmax(h), h.shape)
'The inner boundary is centered at ({} px, {} px); its radius is {} px.'.format(row, col, radius)

'The inner boundary is centered at (219 px, 217 px); its radius is 208 px.'

The radius of the inner boundary turns out to be exactly 208 pixels! For visual inspection, this circle is overlaid on top of the original image (adapted from this scikit-image example).

img_rgb = gray2rgb(img_as_ubyte(img))
rows, cols = circle_perimeter(row, col, radius, method='andres')
img_rgb[rows, cols] = (255, 0, 0)
imsave(os.path.join(root, 'rice-bin_4x4x4-boundary-099.png'), img_rgb)

Which produces the following image (see Fig. 4).

A closer look (see Fig. 5) shows that we roughly achieved pixel accuracy, which will be sufficient for the analysis to come.

Analysis of the whole stack

We are now ready to carry out the above analysis on all 172 images of the stack. This is what the script below does (download); in order to check that nothing went wrong, each image with overlaid boundary is saved for visual inspection.

import os.path
import numpy as np

from skimage.color import gray2rgb
from skimage.draw import circle_perimeter
from skimage.feature import canny
from skimage.io import imread, imsave
from skimage.transform import hough_circle
from skimage.util import img_as_ubyte


def find_boundary(img, min_radius, max_radius):
    edges = canny(img, sigma=0.)
    radii = np.arange(min_radius, max_radius)
    h = hough_circle(edges, radii)
    h_max = np.max(h, axis=(1, 2))
    k = np.min(np.argsort(h_max)[-2:])
    radius = radii[k]
    h = h[k, ...]
    row, col = np.unravel_index(np.argmax(h), h.shape)
    return row, col, radius


def draw_boundary(img, row, col, radius):
    img_rgb = gray2rgb(img_as_ubyte(img))
    rows, cols = circle_perimeter(row, col, radius, method='andres')
    img_rgb[rows, cols] = (255, 0, 0)
    return img_rgb


if __name__ == '__main__':
    root = os.path.join('F:', 'sebastien', 'experimental_data', 'navier', 'riz')
    input_dir = os.path.join(root, 'bin_4x4x4')
    output_dir = os.path.join(root, 'boundary')
    input_name = 'rice-bin_4x4x4-{0:03d}.tif'
    output_name = 'rice-bin_4x4x4-boundary-{0:03d}.png'
    num_slices = 172
    min_radius = 190
    max_radius = 220

    circle_params = np.zeros((num_slices, 3), dtype=np.uint16)
    for i in range(num_slices):
        img = imread(os.path.join(input_dir, input_name.format(i)))
        circle_params[i] = find_boundary(img, min_radius, max_radius)
        img = draw_boundary(img, *circle_params[i])
        imsave(os.path.join(output_dir, output_name.format(i)), img)
    np.save('./circle_params.npy', circle_params)

This script saves the parameters of each circular boundary in an array, which can be restored for further analysis.

a = np.load(os.path.join(root, 'circle_params.npy'))
print('avg = {}\nstd = {}'.format(a.mean(axis=0), a.std(axis=0)))

avg = [218.89534884 216.97674419 207.88372093]
std = [0.30610341 0.1507149  0.32055927]

Which shows that there is very little variation of the circle parameters across the slices.

Closing words

In this post, we saw how to define the (cylindrical) ROI on our stack of images. To do so, we used the Circle Hough Transform to find circular edges in the slices. In the next instalment of this series, I will start discussing segmentation per se.

Side-note: how to produce animated GIFs

The animated GIF in Fig. 3 was produced with ImageJ. The procedure is

1. Import the image sequence (File → Import → Image Sequence…) called rice-bin_4x4x4-hough-099-*.tif,
2. Image → Stacks → 3D Project…
3. Image → Lookup Tables → Fire
4. File → Save As → Gif

To change the frame rate, use Image → Stacks → Tools → Animation Options…