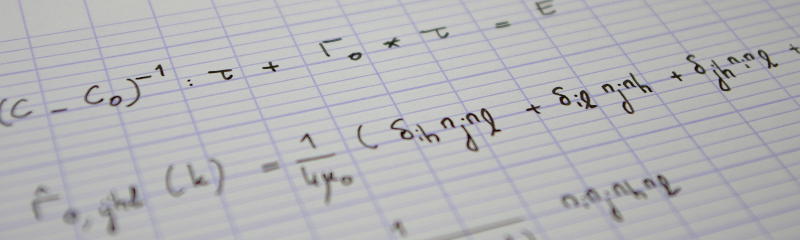In the previous instalment of this series, we discussed the need for periodic images. Although not all images are periodic, some image analysis techniques are best performed in Fourier space (using the fast Fourier transform). Applying Fourier-based techniques to images that are not periodic (as is often the case) generates artifacts. In order to reduce these artifacts, Moisan (2011) proposed to construct a periodic image that is as close as possible to the original image. For reasons that will become clearer in the remainder of this post, he called the resulting construction the “periodic-plus-smooth decomposition”. We will define this decomposition in the remainder of this post, which is the second in a series in seven parts:
- Introduction
- Defining the decomposition
- The energy as a quadratic form
- Implementing the linear operators
- Minimizing the energy, the clumsy way
- Minimizing the energy, the clever way
- Improved implementation of Moisan's algorithm
The code discussed in this series is available as a Python module on GitHub.
As an appetizer, Fig. 1 shows the original image (left) and its periodic (middle) and smooth components (right). Gray levels of the smooth component have been rescaled so as to fit between 0 and 255. Most of this image is grayish, meaning it is zero almost everywhere, except at the boundaries, where it corrects the jumps induced by the lack of periodicity of the initial image.
The decomposition as a minimization problem
Let $u$ be a $m\times n$ image. We want to find two images $p$ (“periodic” component) and $s$ (“smooth” component), such that $u=p+s$ and
- $p$ minimizes jumps across boundaries (periodicity),
- $s$ minimizes jumps between neighbor pixels (smoothness),
- $p$ and $u$ have same mean value (conservation of brigthness).
In Moisan's work, neighbor pixels refer to the 4-connectivity. Furthermore, we define
- direct neighbors, that are adjacent to the pixel under consideration
- indirect neighbors, that are periodic images of these neigbors that would normally fall outside the image.
Fig. 2 illustrates direct and indirect neighbors. It shows that
- corner pixels have 2 direct neighbors and 2 indirect neighbors,
- off-corner, boundary pixels have 3 direct neighbors and 1 indirect neighbor,
- off-boundary (inner) pixels have 4 direct neighbors.
Now, we need to quantify how periodic is $p$, and how smooth is $s$. To do so, we will define two energy functions: $E_\mathrm p$ and $E_\mathrm s$ that penalize lack of periodicity and smoothness, respectively. More precisely, $E_\mathrm p$ (resp. $E_\mathrm s$) is greater for less periodic (resp. less smooth) $p$ (resp. $s$). The periodic-plus-smooth decomposition of an image $u$ is then defined as the pair of images $(p, s)$ that minimize the total energy $E(p, s)=E_\mathrm p(p)+E_\mathrm s(s)$ under the constraints $u=p+s$ and $\operatorname{mean}(s)=0$. The remainder of this post is dedicated to defining the energies $E_\mathrm p$ and $E_\mathrm s$.
How to penalize lack of periodicity?
For each pixel located at the boundary of an image, we compute the sum of squared differences (SSD) with indirect neighbors. The sum of all these SSDs is the energy of the periodic component. Note that direct neighbors are excluded from this sum, as we focus here on the jumps across image boundaries. This leads to the following expression
$$E_\mathrm p(p)=\underbrace{(p_{m-1, 0}-p_{0, 0})^2+(p_{0, n-1}-p_{0, 0})^2}_\text{top-left corner}$$ $$+\underbrace{(p_{0, 0}-p_{0, n-1})^2+(p_{m-1, n-1}-p_{0, n-1})^2}_\text{top-right corner}$$ $$+\underbrace{(p_{0, 0}-p_{m-1, 0})^2+(p_{m-1, n-1}-p_{m-1, 0})^2}_\text{bottom-left corner}$$ $$+\underbrace{(p_{0, n-1}-p_{m-1, n-1})^2+(p_{m-1, 0}-p_{m-1, n-1})^2}_\text{bottom-right corner}$$ $$+\underbrace{\sum_{i=1}^{m-2}(p_{i, n-1}-p_{i, 0})^2}_\text{left column}+\underbrace{\sum_{i=1}^{m-2}(p_{i, 0}-p_{i, n-1})^2}_\text{right column}$$ $$+\underbrace{\sum_{j=1}^{n-2}(p_{m-1, j}-p_{0, j})^2}_\text{top row}+\underbrace{\sum_{j=1}^{n-2}(p_{0, j}-p_{m-1, j})^2}_\text{bottom row},$$
which reduces to
$$E_\mathrm p(p)=2\sum_{i=0}^{m-1}(p_{i, n-1}-p_{i, 0})^2+2\sum_{j=0}^{n-1}(p_{m-1, j}-p_{0, j})^2.$$
How to penalize lack of smoothness?
At this point, you might have guessed that smoothness is measured through the sum of squared differences between direct neighbors
$$E_\mathrm s(s)=\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}\bigl[(s_{i, j-1}-s_{i, j})^2+(s_{i, j+1}-s_{i, j})^2+(s_{i-1, j}-s_{i, j})^2+(s_{i+1, j}-s_{i, j})^2\bigr],$$
where we have defined the following ghost cells
$$s_{i, -1}=s_{i, 0}, \quad s_{i, n}=s_{i, n-1}, \quad s_{-1, j}=s_{0, j} \quad\text{and}\quad s_{m, j}=s_{m-1, j},$$
in order to make sure that indirect neighbors are indeed excluded. It is readily observed that in the above sum, each pair of direct neighbors appears exactly twice. In other words,
$$E_\mathrm s(s)=2\sum_{i=0}^{m-2}\sum_{j=0}^{n-1}(s_{i+1, j}-s_{i, j})^2 +2\sum_{i=0}^{m-1}\sum_{j=0}^{n-2}(s_{i, j+1}-s_{i, j})^2.$$
Python implementation
Implementation of the total energy $E(p, s)=E_\mathrm p(p)+E_\mathrm s(s)$ is
fairly trivial (note the use of the broadcast_arrays function).
def ssd(a, b):
"""Sum of squared differences."""
delta2 = b-a
delta2 *= delta2
return np.sum(delta2)
def energy(p, s):
"""Return the total energy of the periodic-plus-smooth decomposition.
The periodic and smooth components p and s are 2D arrays of
float64. They should have the same shape, although this is not
required by this function. 2D arrays.
The energy is defined in Moisan (2011), Theorem 1. The
contribution of the periodic component is
E_p(p) = sum sum [p(x)-p(y)]**2,
x y
where the first sum is carried over all boundary pixels x, and the
second sum is carried over the indirect neighbors y of x. The
contribution of the smooth component is
E_s(s) = sum sum [s(x)-s(y)]**2,
x y
where the first sum is carried over all pixels x, and the second
sum is carried over the direct neighbors y of x. The total energy
is then defined as
E(p, s) = E_p(p) + E_s(s).
"""
p, s = np.broadcast_arrays(p, s)
return 2*(ssd(p[:, 0], p[:, -1]) +
ssd(p[0, :], p[-1, :]) +
ssd(s[:-1, :], s[1:, :]) +
ssd(s[:, :-1], s[:, 1:]))
An equivalent, unconstrained minimization problem
The periodic-plus-smooth decomposition $(p, s)$ of an image $u$ is defined as the minimizer of the above defined energy $E(p, s)$, under the constraints: $u=p+s$ and $\operatorname{mean}s=0$. Moisan (2011) reformulates this constrained minimization problem as the following unconstrained minimization problem
$$s=\operatorname*{arg\,min}_v F(v, u), \quad\text{with}\quad F(s, u)=E_\mathrm p(u-s)+E_\mathrm s(s)+(\operatorname{mean}s)^2,$$
and the periodic component $p$ reads: $p=u-s$. This is the minimization problem that we will eventually solve.
Conclusion
In the present post, we have defined the periodic-plus-smooth decomposition as the minimizer of Moisan's energy, under the constraint that the average gray level of the periodic component is equal to the average gray level of the initial image.
Moisan (2011) showed that this minimizer is explicit in Fourier space. In the next instalment of this series, we will however temporarily ignore this result, and optimize the total energy in the real space, using standard iterative techniques. This will allow us to generate reference decompositions that will eventually be used to set up unit tests in order to check our implementation of Moisan's method.