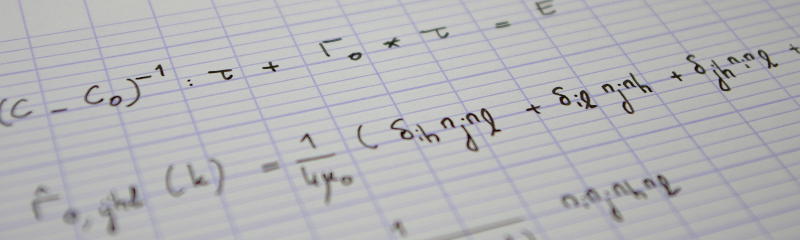In the previous instalment of this series, we introduced the periodic-plus-smooth decomposition of an image as a pair of images which minimizes an energy functional. Observing that this energy is a quadratic form, the purpose of this post is to derive closed form expressions of the underlying linear operators. These expressions will then be combined in the next instalments to a conjugate gradient algorithm in order to minimize the energy of the periodic-plus-smooth decomposition.
This post is the third instalment of a series in seven parts:
- Introduction
- Defining the decomposition
- The energy as a quadratic form
- Implementing the linear operators
- Minimizing the energy, the clumsy way
- Minimizing the energy, the clever way
- Improved implementation of Moisan's algorithm
The code discussed in this series is available as a Python module on GitHub.
In this post, it will be convenient to regard images as vectors. Given two $m\times n$ images $u$ and $v$, the scalar product $\langle u, v\rangle$ is then defined as
$$\langle u, v\rangle=\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}u_{ij}v_{ij}.$$
Likewise, a linear operator $A$ over the space of $m\times n$ images is defined as follows
$$v=A\cdot u,\quad\text{with}\quad v_{ij}=\sum_{k=0}^{m-1}\sum_{l=0}^{n-1}A_{ij,kl}u_{kl}.$$
According to Moisan (2011), the total energy $E(p, s)$ of the periodic-plus-smooth decomposition of an image $u=p+s$ is defined as the sum $E(p, s)=E_\mathrm p(p)+E_\mathrm s(s)$ (see previous instalment), and the smooth component $s$ is the solution to the following minimization problem
$$s=\operatorname*{arg\,min}_v F(v, u),$$
with
$$F(v, u)=E_\mathrm p(u-v)+E_\mathrm s(v)+(\operatorname{mean}v)^2.$$
Introducing the linear operators $Q_1$ and $Q$ such that
$$\langle v, Q_1\cdot v\rangle=E_\mathrm p(v) \quad\text{and}\quad \langle v, Q\cdot v\rangle =E_\mathrm p(v)+E_\mathrm s(v)+(\operatorname{mean}v)^2,$$
it is readily found that
$$F(v, u)=\langle v, Q\cdot v\rangle-2\langle v, Q_1\cdot u\rangle +\langle u, Q_1\cdot u\rangle.$$
The closed-form expression of $Q_1$ is derived in the first part of this post. Then, operator $Q$ is derived in the second part of this post.
Derivation of the Q1 operator
The contribution to the total energy of the periodic component $p$ is defined by Moisan (2011) as follows (see also previous post)
$$E_\mathrm p(p)=2\sum_{i=0}^{m-1}(p_{i, n-1}-p_{i, 0})^2 +2\sum_{j=0}^{n-1}(p_{m-1, j}-p_{0, j})^2.\tag{1}$$
In order to transform the first term, we observe that, $u$ and $v$ being two $m\times n$ images
$$\sum_{i=0}^{m-1}(u_{i, n-1}-u_{i, 0})(v_{i, n-1}-v_{i, 0})$$ $$=\sum_{i=0}^{m-1}u_{i, 0}(v_{i, 0}-v_{i, n-1}) +\sum_{i=0}^{m-1}u_{i, n-1}(v_{i, n-1}-v_{i, 0})$$ $$=\tfrac12\langle u, Q_1^\mathrm h\cdot v\rangle,\tag{2}$$
where we have introduced the linear operator $Q_1^\mathrm h$ defined as follows
$$\tfrac12(Q_1^\mathrm h\cdot u)_{ij}= \left\{ \begin{array}{ll} u_{i, 0}-u_{i, n-1} & \text{if }j=0,\\ u_{i, n-1}-u_{i, 0} & \text{if }j=n-1,\\ 0 & \text{otherwise}. \end{array} \right. \tag{3}$$
From the left-hand side of Eq. (2), the linear operator $Q_1^\mathrm h$ thus defined is obviously symmetric and positive. Besides, the first term in Eq. (1) reads
$$2\sum_{i=0}^{m-1}(p_{i, n-1}-p_{i, 0})^2=\langle p, Q_1^\mathrm h\cdot p\rangle.$$
Turning now to the second term in Eq. (1), we introduce the symmetric, positive linear operator $Q_1^\mathrm v$ defined by
$$\tfrac12(Q_1^\mathrm v\cdot u)_{ij}=\left\{\begin{array}{ll} u_{0, j}-u_{m-1, j} & \text{if }i=0,\\ u_{m-1, j}-u_{0, j} & \text{if }i=m-1,\\ 0 & \text{otherwise}, \end{array}\right.\tag{4}$$
so that
$$2\sum_{j=0}^{n-1}(p_{m-1, j}-p_{0, j})^2=\langle p, Q_1^\mathrm v\cdot p\rangle.$$
Gathering the above results and introducing the symmetric operator $Q_1=Q_1^\mathrm h+Q_1^\mathrm v$, we finally find that $E_\mathrm p(p)=\langle p, Q_1\cdot p\rangle$.
Derivation of the Q operator
The contribution to the total energy of the smooth component $s$ is defined by Moisan (2011) as follows (see also previous post)
$$E_\mathrm s(s)=2\sum_{i=0}^{m-2}\sum_{j=0}^{n-1}(s_{i+1, j}-s_{i, j})^2 +2\sum_{i=0}^{m-1}\sum_{j=0}^{n-2}(s_{i, j+1}-s_{i, j})^2.\tag{5}$$
In the present section, all $m\times n$ images $v$ will be extended by periodicity as follows
$$v_{i, -1}=v_{i, n-1}, \quad v_{i, n}=v_{0, n}, \quad v_{-1, j}=v_{m-1, j}\quad\text{and}\quad v_{m, j}=v_{0, j}.\tag{6}$$
Combining Eqs. (1) and (5), it is found that
$$E_\mathrm p(v)+E_\mathrm s(v) =2\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}(v_{i+1, j}-v_{i, j})^2 +2\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}(v_{i, j+1}-v_{i, j})^2, \tag{7}$$
In order to transform the first term in Eq. (7), we observe that, $u$ and $v$ being two $m\times n$ images that are both extended according to Eq. (6)
$$\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}(u_{i+1, j}-u_{i, j})(v_{i+1, j}-v_{i, j})$$ $$=\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}u_{i+1, j}(v_{i+1, j}-v_{i, j}) -\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}u_{i, j}(v_{i+1, j}-v_{i, j})$$ $$=\sum_{i=1}^m\sum_{j=0}^{n-1}u_{i, j}(v_{i, j}-v_{i-1, j}) -\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}u_{i, j}(v_{i+1, j}-v_{i, j})$$ $$=\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}u_{i, j}(v_{i, j}-v_{i-1, j})-\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}u_{i, j}(v_{i+1, j}-v_{i, j})$$ $$=\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}u_{i, j}(2v_{i, j}-v_{i-1, j}-v_{i+1,j})$$ $$=\tfrac12\langle u, Q^\mathrm h\cdot v\rangle,\tag{8}$$
where we have introduced the linear operator $Q^\mathrm h$ defined as follows [see Eq. (6)]
$$\tfrac12(Q^\mathrm h\cdot u)_{i,j}=2u_{i, j}-u_{i-1, j}-u_{i+1,j}.\tag{9}$$
From the left-hand side of Eq. (7), the linear operator $Q^\mathrm h$ thus defined is obviously symmetric and positive. Besides, the first term in Eq. (7) reads
$$2\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}(v_{i+1, j}-v_{i, j})^2 =\langle v, Q^\mathrm h\cdot v\rangle.$$
Turning now to the second term in Eq. (5), we introduce the symmetric, positive linear operator $Q^\mathrm v$ defined by
$$\tfrac12(Q^\mathrm v\cdot u)_{i,j}=2u_{i, j}-u_{i, j-1}-u_{i,j+1},\tag{10}$$
so that
$$2\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}(v_{i, j+1}-v_{i, j})^2=\langle v, Q^\mathrm v\cdot v\rangle.$$
Finally
$$(\operatorname{mean}u)(\operatorname{mean}v)=\frac{\operatorname{mean}v}{mn}\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}u_{i,j}$$ $$=\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}u_{i,j}\times\frac{\operatorname{mean}v}{mn}=\langle u, Q^\mathrm m\cdot v\rangle,\tag{11}$$
where we have introduced the symmetric, positive operator $Q^\mathrm m$ defined as follows
$$(Q^\mathrm m\cdot v)_{i,j}=\frac{\operatorname{mean} v}{mn}=\frac1{m^2n^2}\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}v_{i,j}.\tag{12}$$
Gathering the above results and introducing the symmetric, positive operator $Q=Q^\mathrm h+Q^\mathrm v+Q^\mathrm m$, we finally find that $E_\mathrm p(v)+E_\mathrm s(v)+(\operatorname{mean} v)^2 =\langle s, Q\cdot s\rangle$.
Conclusion
In this post, we have defined two linear operators, namely $Q_1$ and $Q$, that operate on the space of $m\times n$ images, and such that
$$F(v, u)=\langle v, Q\cdot v\rangle-2\langle v, Q_1\cdot u\rangle+\langle u, Q_1\cdot u\rangle,$$
where the minimizer of $F$ with respect to its first argument $v$ is the smooth component $s$ of $u$ (the periodic component $p$ is then obtained from $p=u-s$). In the next instalment of this series, we will proceed to implement $Q_1$ and $Q$ in Python. To do so, we will adopt a matrix-free approach.