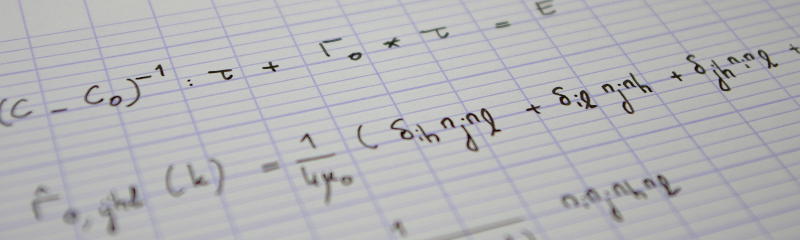In the previous instalment of this series, we introduced the linear operators $Q_1$ and $Q$ that allow to define Moisan's (2011) periodic-plus-smooth decomposition $(p, s)$ of an image $u$ as follows
$$s=\operatorname*{arg\,min}_v F(v, u)\quad\text{and}\quad p=u-s,$$
with
$$F(v, u)=\langle v, Q\cdot v\rangle-2\langle v, Q_1\cdot u\rangle+\langle u, Q_1\cdot u\rangle.$$
In theory, the linear operators $Q_1$ and $Q$ are matrices. However, for
$m\times n$ images, these matrices would be unnecessarily large: $mn\times mn$!
We will therefore adopt here a matrix-free
approach for the Python
implementation of these operators. The remainder of this post is organized as
follows. We will first discuss linear operators in the
scipy.sparse.linalg sense. Then, we will implement the $Q_1$ operator
and the $Q$ operator. Finally, we will test our
implementation.
This post is the fourth instalment of a series in seven parts:
- Introduction
- Defining the decomposition
- The energy as a quadratic form
- Implementing the linear operators
- Minimizing the energy, the clumsy way
- Minimizing the energy, the clever way
- Improved implementation of Moisan's algorithm
The code discussed in this series is available as a Python module on GitHub.
Matrix-free linear operators
The $Q_1$ and $Q$ linear operators will be implemented as instances of
LinearOperator from the scipy.sparse.linalg module (see
documentation).
Essentially, what this means is that $Q_1$ and $Q$ are seen as functions
(linear maps) that perform the matrix-vector product. Often times, this is
enough to perform fairly complex linear algebra operations. In particular,
solving linear systems that involve $Q_1$ and $Q$ can then be done by means of
iterative linear
solvers, such as
the conjugate gradient
method. Interesting
references on this topic are the book by Y. Saad: Iterative Methods for Sparse
Linear Systems and the book by Barrett
et al.: Templates for the Solution of Linear Systems: Building Blocks for
Iterative Methods (also
freely available here).
It should be noted that instances of LinearOperator (in the Scipy sense)
operate on 1D vectors. Therefore, 2D images must be converted to 1D vectors each
time linear operators are to be invoked. We will assume C-ordering in the
implementation below. We first create the base class ImageLinearOperator, that
defines linear operators for images, the shape of which is stored in the
class. This class will be used below to implement the operators $Q_1$ and $Q$.
class ImageLinearOperator(scipy.sparse.linalg.LinearOperator):
"""Linear operator that operate on images.
This class defines a linear operator (in the SciPy sense) that
operates on n-dimensional images, the shape of which is passed to
the initializer
>>> a = ImageLinearOperator((10, 5))
>>> a.img_shape
(10, 5)
>>> a.shape
(50, 50)
SciPy linear operators operate on one-dimensional vectors: the
methods _matvec and _adjoint implemented by each subclass must
therefore first reshape the input array to a n-dimensional
image. By convention, C-ordering will always be assumed.
y = numpy.zeros_like(x)
x2 = x.reshape(self.img_shape)
y2 = y.reshape(self.img_shape)
......................
# Operate on x2 and y2
......................
return y
Alternatively, developers may implement the method _apply that
operates on n-dimensional images: the default implementation of
_matvec calls this method on the input vector, suitably reshaped to
a n-dimensional image.
"""
def __init__(self, img_shape, dtype=np.float64):
self.img_shape = img_shape
n = np.product(self.img_shape)
shape = (n, n)
super(ImageLinearOperator, self).__init__(dtype, shape)
def _matvec(self, x):
y = np.zeros_like(x)
x2 = x.reshape(self.img_shape)
y2 = y.reshape(self.img_shape)
self._apply(x2, y2)
return y
def _apply(x, y=None):
"""Apply this operator on the input image x.
The shape of x must be self.img_shape. The returned array has
same shape as x.
If specified, the optional argument y must be an array of same
shape as x. It is modified in-place, and a reference to y is
returned.
"""
raise NotImplementedError()
Implementation of the $Q_1$ operator
The $Q_1$ operator was defined in the previous post as the following sum: $Q_1=Q_1^\mathrm h+Q_1^\mathrm v$, with
$$\tfrac12(Q_1^\mathrm h\cdot u)_{ij}=\left\{\begin{array}{ll}u_{i, 0}-u_{i, n-1} & \text{if }j=0,\\ u_{i, n-1}-u_{i, 0} & \text{if }j=n-1,\\ 0 & \text{otherwise}\end{array}\right.$$
and
$$\tfrac12(Q_1^\mathrm v\cdot u)_{ij}=\left\{\begin{array}{ll}u_{0, j}-u_{m-1, j} & \text{if }i=0,\\u_{m-1, j}-u_{0, j} & \text{if }i=m-1,\\0 & \text{otherwise}\end{array}\right.$$
Implementation is fairly simple; note that $Q_1$ is symmetric: the _adjoint()
method simply returns self.
class OperatorQ1(ImageLinearOperator):
"""Implementation of Q1 as a ImageLinearOperator.
Q1 is defined by Eq. (9) of Moisan (2011)
F(s) = <u-s, Q1.(u-s)> + <s, Q2.s>,
where F(s) is the function to be minimized with respect to the
smooth component s. F is defined by Eq. (8)
F(s) = E(u-s, s) + mean(s)**2,
so that
<v, Q1.v> = E(v, 0) and <v, Q2.v> = E(0, v) + mean(v)**2.
Image p = u-s must be passed as a 1-dimensional vector. Internally,
it is reshaped to a two-dimensional image (the shape of which is
passed to the initializer), assuming C-ordering.
"""
def __init__(self, img_shape, dtype=np.float64):
super(OperatorQ1, self).__init__(img_shape, dtype)
def _apply(self, x, y=None):
if y is None:
y = np.zeros_like(x)
dx = 2*(x[:, 0]-x[:, -1])
y[:, 0] = dx
y[:, -1] = -dx
dx = 2*(x[0, :]-x[-1, :])
y[0, :] += dx
y[-1, :] -= dx
return y
def _adjoint(self):
return self
Implementation of the $Q$ operator
The $Q$ operator was defined in the previous post as the following sum: $Q=Q^\mathrm h+Q^\mathrm v+Q^\mathrm m$, with
$$\tfrac12(Q^\mathrm h\cdot u)_{ij}=2v_{ij}-u_{i-1, j}-u_{i+1,j},$$ $$\tfrac12(Q^\mathrm v\cdot u)_{ij}=2v_{i, j}-u_{i, j-1}-u_{i,j+1},$$ $$(Q^\mathrm m\cdot u)_{ij}=\frac1{m^2n^2}\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}u_{ij},$$
where the following ghost cells have been defined
$$u_{i, -1}=u_{i, n-1}, \quad u_{i, n}=u_{0, n}, \quad u_{-1, j}=u_{m-1, j}\quad\text{and}\quad u_{m, j}=u_{0, j}.$$
It is readily seen that $(Q^\mathrm h+Q^\mathrm v)\cdot u$ is the periodic convolution of $u$ with the following kernel
$$\begin{bmatrix} 0 & -2 & 0\\ -2 & 8 & -2\\ 0 & -2 & 0 \end{bmatrix}.$$
Operator $Q$ is then readily implemented. Observe again that $Q$ being
symmetric, _adjoint() returns self.
class OperatorQ(ImageLinearOperator):
"""Implementation of Q = Q1+Q2 as a ImageLinearOperator.
Q1 and Q2 are defined by Eq. (9) of Moisan (2011)
F(s) = <u-s, Q1.(u-s)> + <s, Q2.s>,
where F(s) is the function to be minimized with respect to the
smooth component s. F is defined by Eq. (8)
F(s) = E(u-s, s) + mean(s)**2,
so that
<v, Q1.v> = E(v, 0) and <v, Q2.v> = E(0, v) + mean(v)**2.
Image s must be passed as a 1-dimensional vector. Internally, it is
reshaped to a two-dimensional image (the shape of which is passed
to the initializer), assuming C-ordering.
"""
def __init__(self, img_shape, dtype=np.float64):
super(OperatorQ, self).__init__(img_shape, dtype)
self.kernel = np.array([[0, -2, 0],
[-2, 8, -2],
[0, -2, 0]], dtype=dtype)
def _apply(self, x, y=None):
if y is None:
y = np.zeros_like(x)
scipy.ndimage.convolve(x, self.kernel, output=y, mode='wrap')
return y+x.mean()/self.shape[0]
def _adjoint(self):
return self
Note that in the above implementation, attention is paid to the definition of
the kernel, which is of the same dtype as the images to which the operator is
to be applied. This allows for exact computations on integer images.
Testing the implementation
For any image $v$, we should have
$$\langle v, Q_1\cdot v\rangle=E(v, 0)\quad\text{and}\quad\langle v, Q\cdot v\rangle=E(v, 0)+E(0, v)+(\operatorname{mean} v)^2,$$
where the energy $E$ was implemented in part 2 of this series.
def img_shapes():
sizes = (16, 17, 32, 33)
return itertools.product(sizes, sizes)
@pytest.mark.parametrize('shape', list(img_shapes()))
def test_OperatorQ(shape):
np.random.seed(20180125)
q = moisan2011.OperatorQ(shape, dtype=np.int64)
# Force non-zero mean
u1 = (np.random.randint(-128, 128)
+ np.random.randint(-128, 128, size=q.shape[0:1], dtype=np.int64))
u1[0] -= np.sum(u1) % u1.shape[0]
u2 = u1.reshape(shape)
expected = moisan2011.energy(u2, 0)+moisan2011.energy(0, u2)
actual = np.dot(q.matvec(u1), u1)
assert_array_equal(actual, expected)
@pytest.mark.parametrize('shape', list(img_shapes()))
def test_OperatorQ1(shape):
np.random.seed(20180125)
q = moisan2011.OperatorQ1(shape, dtype=np.int64)
p1 = np.random.randint(-128, 128, size=(q.shape[0],), dtype=np.int64)
p2 = p1.reshape(shape)
expected = moisan2011.energy(p2, 0)
actual = np.dot(q.matvec(p1), p1)
assert_array_equal(actual, expected)
The above code snippet calls for several remarks
- We used the great pytest library to write the unit tests: this allows for parameterized tests.
- The seed of the random generator is fixed: this ensures reproducibility.
- Non-square images were used: this allows for the detection of some silly errors, such as rows and columns swapping.
- Integer images were used: exact equality can then be asserted.
Conclusion
In this post, we have implemented the linear operators $Q_1$ and $Q$. We are now in a position to (at last!) compute the periodic-plus-smooth decomposition of an image. This will be done in the next instalment of this series