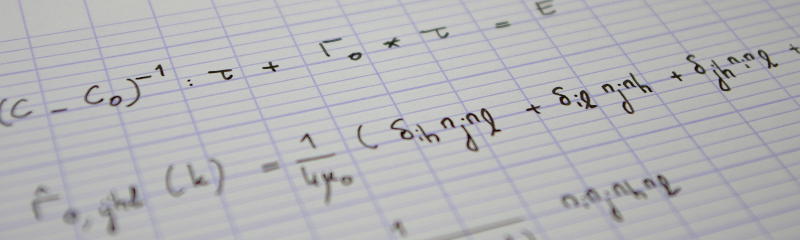Articles in the Image analysis category

In the previous instalment of this series, we implemented Moisan's (2011) efficient algorithm to compute the periodic-plus-smooth decomposition of an image. This algorithm relies heavily on the discrete Fourier transform, and already improves quite a lot over our previous conjugate gradient-based implementation. In the present post, we will show that …

In the previous instalment of this series, we computed Moisan's (2011) periodic-plus-smooth decomposition of an image by means of the conjugate gradient method. This worked like a charm, but was fairly inefficient, owing to the iterative nature of the method. Moisan actually showed that the whole decomposition could be computed …

In this post, we will compute Moisan's (2011) periodic-plus-smooth decomposition of an image by direct minimization of the energy introduced in the second instalment of this series. More precisely, $u$ being a $m\times n$ image, we will minimize the function $F(v, u)$ over the space of $m\times …

In the previous instalment of this series, we introduced the linear operators $Q_1$ and $Q$ that allow to define Moisan's (2011) periodic-plus-smooth decomposition $(p, s)$ of an image $u$ as follows

$$s=\operatorname*{arg\,min}_v F(v, u)\quad\text{and}\quad p=u-s,$$

with

$$F(v, u …

In the previous instalment of this series, we introduced the periodic-plus-smooth decomposition of an image as a pair of images which minimizes an energy functional. Observing that this energy is a quadratic form, the purpose of this post is to derive closed form expressions of the underlying linear operators. These …

In the previous instalment of this series, we discussed the need for periodic images. Although not all images are periodic, some image analysis techniques are best performed in Fourier space (using the fast Fourier transform). Applying Fourier-based techniques to images that are not periodic (as is often the case) generates …

In this new series, we will explore the so-called periodic-plus-smooth decomposition of an image, introduced by Moisan in 2011. This series is largely based on Moisan's paper, called Periodic plus Smooth Image Decomposition (the author's version can be found on HAL). Besides introducing a quite smart technique (that I do …

In the previous instalment of this series, we have analyzed the morphology of the rice grains. In particular, we have defined their orientation as that of the major axis of inertia. We are now in a position to quantify the statistics of the orientations. We will first discuss one-point statistics …

$\newcommand{\tens}{\mathbf}\newcommand{\D}{\mathrm{d}}$

In the previous instalment of this series, we have segmented the 3D image of the assembly of rice grains. In other words, each voxel of the image is attributed the label of the grain to which it belongs. Remember the initial goal of …

In the previous instalment of this series, I showed that a convincing binary image could be produced from the gray level 3D reconstruction of the assembly of rice grains, using Otsu's threshold. However, I intend to carry out statistical analyses of the grains themselves in the subsequent instalments. Therefore, instead …

In the previous instalment of this series, we used the circle Hough transform to find the boundary of the sample and define the circular ROI. Within this ROI, we now need to segment the rice grains. In other words, starting from a gray-level image (Fig. 1, left), we want to …

In the first instalment of this series, I briefly introduced orientational order in assemblies of anisotropic particles, and proposed an illustration based on synthetic microstructures. But what I really intend to do in this series is to show how orientational order can be quantified in a “real-life” sample, namely a …

In this series, I will explore the notion of orientational order in random packings of anisotropic (flat or elongated), hard particles. By orientational order, I mean that particles which are close to each other tend to adopt the same orientation. This leads to strong local anisotropy, while the packing may …